第２章−ミクロの世界の記述：量子力学の基本的な考え方(パターン2-1）

　前章で，電子・原子・分子などミクロの世界に存在する粒子は人間が住むマクロの世界の常識を超えたふるまいをすることを述べ，それらの不思議な現象は量子力学を使えば論理的に，定量的に，統一的に説明できることを述べた。(ムービー2-1,2-2)

本章では量子力学の根幹となるシュレーディンガーの波動方程式を提示し，その基本的な考え方と使い方について要点を絞って説明する。

１．波動方程式への準備

　第１章で述べたようなミクロの現象は，波動方程式を立ててそれを解くことによってはじめて説明できる。その説明に入る前に，まず基礎として「マクロの物体の運動」の古典力学で使われる言葉と内容を簡単にまとめてみる。

力学の初歩を履修したことのない読者は，下記の要点を入門書で学習してほしい。

（１）古典力学における運動の表し方：　１次元１粒子の運動

　質量の物体が１次元（方向）に力Ｆを受けて時刻にの初速で位置から運動を始めたとする。ニュートンの第２運動法則によれば，その物体の加速度は力に比例し，次の微分方程式で表される。

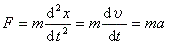(2.1)

また，速度の代わりに運動量がしばしば用いられる。

物体の運動エネルギーは

(2.2)

で定義され，位置エネルギーは

(2.3)

と定義される（はポテンシャルエネルギーともいう。

がこのように定義できるとき，その力を保存力という）。

式(2.3)をで微分すると，

(2.4)

となり，位置エネルギーの傾き（勾配）は力Ｆを表していることがわかる。

二つのエネルギーＴとＶの和は，「（力学的）全エネルギー」あるいは「ハミルトン関数」とよばれ，

(2.5)

と書ける。

とはいずれも時間に依存して変化するが，その和は時間によらない定数Ｅとなる。

この式は「エネルギー保存則」とよばれ，ニュートンの運動法則（時間に関する微分形の表現）と同等な内容を積分形で表したものである。

このとき，物体が持つエネルギーの値は，初期条件の設定を変えれば，任意の値を連続的にとることができる。これが古典力学の「常識」である。

（２）調和振動子の古典力学（ムービー2-3)

上記の課題の例として，バネの振動の運動エネルギーＴと位置エネルギーＶについて考えてみよう。

この系は調和振動子とよばれ，古典力学で最初に学習する問題の一つである。

質量のないバネに質量の物体をつけて，それを平衡点からまで引っぱって静かに放すと，物体は周期的に振動する。

伸びた距離をとすると，物体を引き戻そうとする力は，変位があまり大きくないとき（すなわち弾性限界までの範囲で），ほぼ正確にに比例する（フックの法則）。

比例定数を力の定数という。

初期条件（ｔ＝0で

、

速さ

）を

設定してニュウ−トンの運動方程式

(2.6)

を解くと，

(2.7)

となり，振動の振幅は時間とともに振動する。

単位時間（１秒）あたりの振動数ν（単位：ヘルツ Hz）は，バネの強さと物体の質量によって決まり，

(2.8)

と表される。

この振動の運動エネルギーと位置エネルギーは，運動量を用いて

(2.9)

(2.10)

と書かれる。

両者の和は(2.5)で説明した全エネルギー（ハミルトン関数）で，

(2.11)

となって，時間によらず振幅だけで決まる（エネルギー保存則）。

　V(x) を距離ｘに対してプロットすると，図２-１の放物線になる。

T(x)は振幅の両端　　　でゼロになり，物体はそこで一時停止して逆戻りをする。この点　　を古典的転回点という。

ｘ＝0でV(ｘ）はゼロになり，T(x)は最大になる。

このように，この物体は全エネルギーをいつも一定に保ち，運動エネルギーと位置エネルギーとを絶えず交換しながら振動する。

物体の最大振幅は　　　　，初めに（すなわちｔ＝0で）物体をどこで放したかで決まるが，その値は任意に連続的に変えることができる。

したがって，その物体が持つエネルギーすなわちハミルトン関数Hの値も連続量になる。

（３）不連続な値をとる物理量の数学的表現法

　ところが，原子・分子のミクロの世界では，「系のエネルギーは多くの場合に特定の不連続な値だけしかとらない」ことが実験の結果として知られている（本章２-(2),(3)参照）。(ムービー2-1,2-2)

そのような「常識はずれの現象」はなぜ起こるのだろう？

この質問には，前章で述べたように「自然はそのように作られている」としか答えられない。

しかしここで明らかなのは，「そのような不連続な値だけしかとれない物理量を数式を使って表現するには，数学的に何か特別な工夫をしなければならない」ことである。

（４）基本法則の模索と発見

　前章で述べたように，ミクロの世界の現象に量子，すなわち不連続に変化する物理量があることをプランクが初めて明らかにしたのは1900年であった。

その後の４半世紀にわたって多くの理論物理学者が真剣に模索したのは，「不連続な値をとる物理量を無理なく表現するにはどんな数学を使えばよいか」とい

う問題だったといってよかろう。

　1926年になってシュレーディンガーは「物理量を演算子で表現する」という素晴らしいアイディアを発表した。(ムービー2-4)

この発想は普通の常識の延長線では考えられない奇抜なものであるが，ひとたびそれを認めれば，そのあとはミクロの世界の現象が無理なく統一的に説明できる魔法のようなものである。

このようにして作られた波動方程式は，われわれがミクロの世界に理論的に踏み込む突破口となった。

（５）演算子と固有値（パターン2-2,2-3,2-4)（ムービー2-4)

演算子とは，ある関数を別の関数に対応させる規則である。あるの関数にその変数

かける演算子　　と，ｘで微分する演算子　　を　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

(2.12)

(2.13)

とする。

演算子であることを明示するために，記号の上に山印をつける。

演算子の積とは，まず右側を演算して次に左側を演算することである。

普通のかけ算と違って，左右を取り替えると同じ演算にならない場合もある。

たとえば

(2.14)

(2.15)

　すなわち，(2.14)と(2.15)のそれぞれ両辺の引き算をすると，

(2.16)

となり，演算子を交換すると１をかける演算をしたことになる。

この簡単な式は，量子力学の基本に関わる「不確定性原理」の表現にも現れる（参考文献参照）。

（６）固有値と固有関数（パターン2-3,2-4）(ムービー2-4)

　量子力学では「演算子の固有値と固有関数」を使う。

たとえば、関数 として指数関数をとり，微分演算子　　を演算すると，結果は

(2.17)

(2.18)

となって，もとの関数に定数　をかける演算と等しい。

このような場合に，定数　　を演算子　　の固有値といい，関数を演算子　　の（固有値　　に対応する）固有関数という。

　次に２次微分演算子の例をあげよう。

この問題はすぐあとの波動方程式で利用する。波動関数を表すのにしばしば用いられるプサイというギリシア文字ψを使って，

(2.19)

という関数を考える＊１。

ｉは虚数単位である。これにを演算すると，

(2.20)

となり，固有値はになる。

この方程式は，一般には固有値が任意の定数のとき成立する。

しかし固有関数に条件がつくと，限定された固有値だけが許されることになる。

この関数ψは，ある半径Ｒの円弧上（図２-２）の波動を表す。

波が一回りして原点に戻ったとき（），関数ψも元に戻ると考えると，次の式が成立する。

(2.21)

(2.22)

(2.23)

(2.24)

すなわち，この２次微分演算子の固有値は，がこのような整数の値をとるときに限って許される。

＊１−−−−−−−−−−−−−−−−−−−−

（2.19）のような虚数の指数関数になじみのない受講生は，ここでまず戸惑うかもしれない。数学の定理によれば

(2.25)

であり，この関数は（時間的あるいは空間的に）周期的な変化をする現象を記述するときに使われる。