3.結合エネルギー
化学結合の強さは,基底状態にある原子を基準とし,結合形成によってどの位の大きさのエネルギーが放出されるかによって示される。
これが結合エネルギーである。
この値は通常モル当りキロジュールkJmol-1で与えられるが,その結合を切断して基底状態の原子にするのに必要なエネルギーと考えてもよい。
(1)結合エネルギーの測定
この値は直接測定出来ることは少なく,生成熱の測定に基づいて間接に求める。
各元素単体の最も安定な状態を標準値0とし,化学変化によりある化合物を生じた時に放出または吸収された熱エネルギーを25℃1気圧での値に換算したものをその化合物の生成熱という。
単体が1気圧25℃で持つ熱エネルギーを0とするのは便宜上である。
このとき吸熱を正に,放熱を負にとる。
化合物の保有するエネルギーの増減として示すためである。
1気圧25℃における単体を同じ条件下での基底状態原子に変えるのに必要なエネルギーも実験的に求められるが,それらはすべて正の値を持つ。
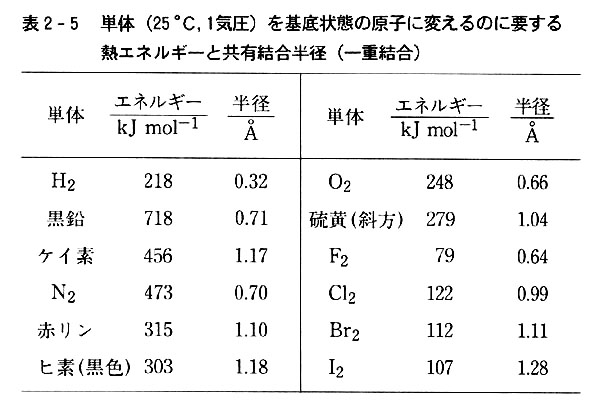
希ガス元素以外の単体は気体でも固体結晶でも,原子間の結合によってそれだけ安定化しているわけである。(表2-5)
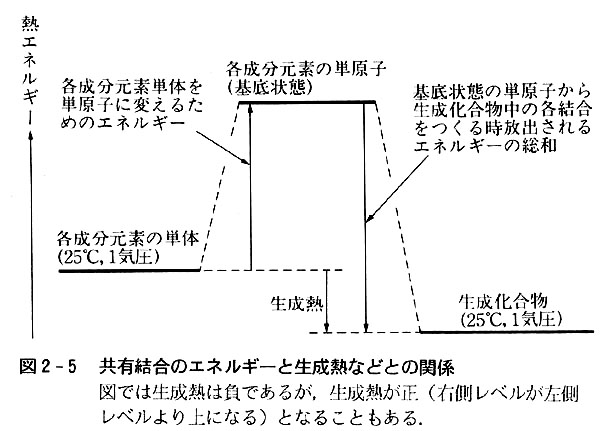
実際に2種以上の単体から化合物を生じる時は複雑な化学反応を経由するが,この時単体がすべて一旦基底状態の原子となり,その原子から当該化合物を生じたとしても,生成熱は同じはずである。
このことはヘスの法則として知られているが,またエネルギー不滅則の一つの現れでもある。
すなわち図2-5の関係が成立する。
この関係を用いると,測定された生成熟と基底状態原子の生成に要する熱エネルギー(表2-5)とから,化合物中の原子間の結合エネルギーの総和が求められる。
例えばメタンの生成熱は−74.5kJmol-1であり,これは1気圧25℃の黒鉛(グラファイト)1モル12.01gと,同条件の水素分子2モルから1モルのメタンを1気圧25℃で作る時,放出された熱エネルギーに当る。
一方,同量の黒鉛をすべて基底状態の炭素原子とするのに要する熱エネルギーは+716.68kJmol-1,2モルの水素分子を4モルの基底状態水素原子に変えるには871.88kJmol-1を要する。
この差引によってC-H結合4個が生じたのだから,ヘスの法則で次式を得る。
4x=[−74.5−(716.68+871.88)](単位kJmol-1)
計算するとx=415.9 kJmol-1となる。ここでの1モルはC-H結合がアボガドロ数だけあることを意味する。
(2)共有結合エネルギーの一般値
個々の化学結合のエネルギーは実験データから求められるが,その値は一定不変なものではなく,各原子が当該結合のほかにどういう結合を持つかによって変化する。
例えばC-H結合エネルギーもメタンとべンゼンとでは少し違うし,酢酸やアルコールではさらに異なる。
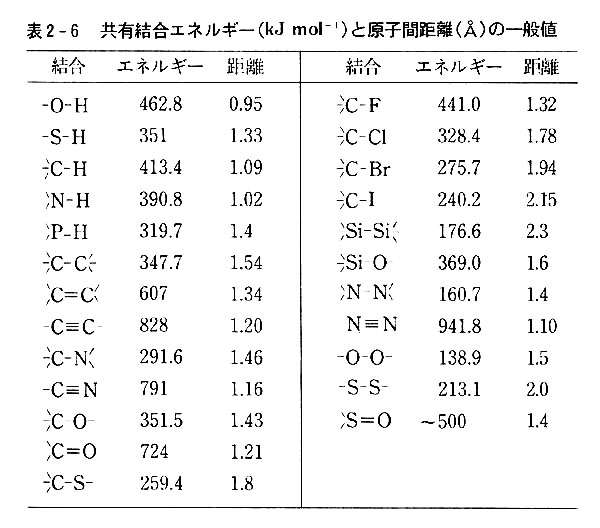
それでも,ある原子間の結合エネルギーの大体の値は,各種の考察に極めて重要であるから,表2-6に示した。表を利用する時には今述べた注意を忘れてはならない。
この値は「見かけの結合エネルギー」というべきものである。
共有結合を考える時に基底状態から原子価状態に励起し,LCAO法を適用することが多い。
基底状態から結合状態に移る時の熱エネルギーは,原子価状態への励起エネルギー(吸熱)と原子価状態から結合状態が生まれる時の放出エネルギーとの差に相当する。
(3)結合エネルギーと原子間距離との関係
共有結合を作っている原子間の距離は正確に測定される。例えばメタンのC-Hは1.0870Å(lÅ=10-10m)であるが,エタノールCH3CH2OHの末端CH3基では1.09,OH基を持つCH2上では1.10Åである。
各原子に結合した他原子の種類によって値が変化する。
一方C-H上でどこまでがCの,どこからがHの領域かを決定することは困難である。
しかし便宜的に,炭素原子の半径はこの位,水素原子ではこの位という値を知ることは極めて有益である。
表2-6には各原子間の距離を,表2-5には共有結合を作る半径を与えた。
同じ炭素原子でも,C-Cの時と,C=C二重結合の時とでは大差がある。
これらの値は結合半径というのが正しい。
原子がイオンになった時のイオン半径(第8回)はさらに異なった値である。
表で見るとおり,原子間距離が短いほど結合エネルギーが増加するのが一般則である。
原子の種類に関係なく,原子どうしが近づく程原子間には強い結合力が働き,安定化するわけである。
資料提供 分子科学研究所教授 廣田 栄治


