4.理想気体の分子運動論
●状態方程式
気体分子が質点として空間を自由に運動するモデルで,理想気体の状態方程式を導くことができる.
いま,一辺Lの立方体の中で質量mの分子が,質点として自由運動している場合を考える.
分子間に力が働かないから,各分子の運動は独立である.
立方体の中にアボガドロ定数個の分子が入っているとすると,図1-4の立方体のyz面に分子が衝突する頻度は,x方向の速度成分vxを使って,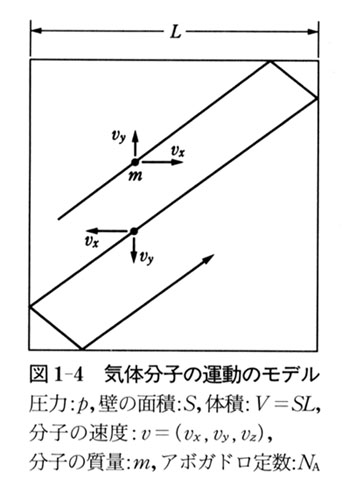
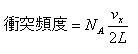 (1.5)
(1.5)
となる.
すると,1回の衝突での運動量変化は,2mvxであるから単位時間当りの運動量変化
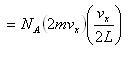 (1.6)
(1.6)
で,これは壁に加わる力に等しい.
圧力をp,壁の面積をSとすれば
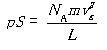 (1.7)
(1.7)
である.
すると,体積V = SLであるから
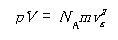 (1.8)
(1.8)
となる.
いま,分子の平均の連動エネルギーを
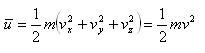 (1.9)
(1.9)
と定義すると,分子の運動はx,y,z方向に均等に行われるので,
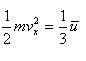 (1.10)
(1.10)
である.
すると,(1.8)式は,
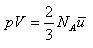 (1.11)
(1.11)
である.
いま,1モルの平均運動エネルギーUを定義すると,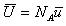 で,
で,
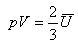 (1.12)
(1.12)
となる.
(1.8)式,または,(1.9)式を理想気体の状態方程式
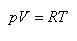 (1.13)
(1.13)
と比較すると,分子の平均の運動エネルギーを
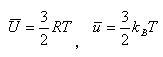 (1.14)
(1.14)
とすれば,気体分子運動論による状態方程式と一致する.
ここで,kBはボルツマン定数で,気体定数と
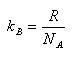 (1.15)
(1.15)
の関係がある.
分子の運動エネルギーは,(1.14)式によれば温度の関数である.
x,y,zの1つの方向についての平均運動エネルギーが(1/2)kBTである.
このことは「エネルギー等分配の原則」に由来するが,これについては,次章で再び触れることにする.
アボガドロの仮説は,「気体中で分子が質点として独立に運動する」ということと等価であることが判明した.
そのために,気体の体積は分子の種類によらずに一定なのである.
アボガドロは,理想気体の状態方程式を通して質点として振る舞う分子を観察したといってよい.
ここで,特に注意するべきことは,(1.15)式である.
気体定数は,気体の温度,圧力や体積のマクロな量の観測によって測定することができる.
一方,ボルツマン(L. Boltzmann)が導入したボルツマン定数は気体分子1個1個の運動に関係する定数である.
その意義については,後にもう一度学ぶことにするが,二つの定数を結ぶ定数がアボガドロ定数である.
アボガドロの時代にそれを定めることはできなかったが,その値は
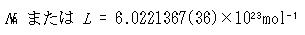
である.
ここで,Lは,単位体積の気体中の分子数を1865年に初めて計算したロシュミット(J. Loschmidt)を記念した記号である.
●分子の運動速度
気体分子の平均運動エネルギーが(1.14)式のように絶対温度に比例することを実験で確かめることができる.
それには気体分子の速度を直接測定すればよい.
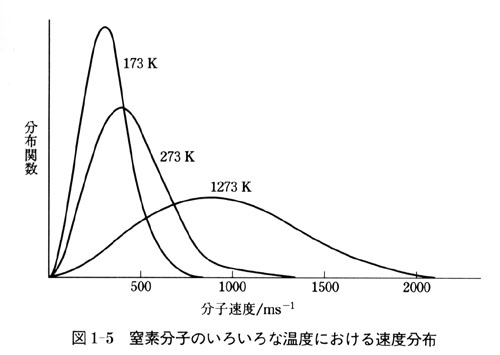
図1-5に窒素分子の速度の分布状態を示した.
温度が高いと,速度の分布は広い範囲にわたるが,速度分布のピーク近傍に速度の2乗平均値があり,その値は(1.14)式より予測される.
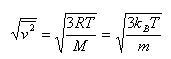 (1.16)
(1.16)
である.
なお,ここでMは分子量,mは分子の質量である.
したがって,低い温度では,分子の速度は小さくなり,速度分布は比較的狭い速度領域に限定される.
気体分子の速度分布は,後に触れる統計力学の方法で温度の関数で表すことができる.このことについては付録5を参照するとよい.

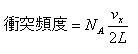 (1.5)
(1.5)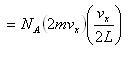 (1.6)
(1.6)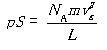 (1.7)
(1.7)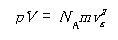 (1.8)
(1.8)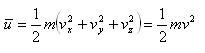 (1.9)
(1.9)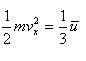 (1.10)
(1.10)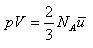 (1.11)
(1.11)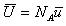 で,
で,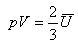 (1.12)
(1.12)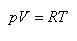 (1.13)
(1.13)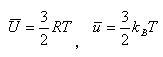 (1.14)
(1.14)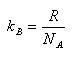 (1.15)
(1.15)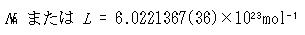

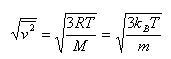 (1.16)
(1.16)