4.熱容量
●定義
系の温度を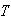 から
から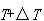 に上昇させるとき系が外界から吸収する熱を
に上昇させるとき系が外界から吸収する熱を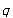 とする.
とする.
温度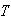 において,系の温度を単位だけ上昇させるのに必要な熱を熱容量と呼び,次のように定義される.
において,系の温度を単位だけ上昇させるのに必要な熱を熱容量と呼び,次のように定義される.
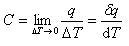 (2.7)
(2.7)
系の熱容量は加熱の条件によって異なる.
体積一定の条件で,温度上昇させるときの熱容量を定積熱容量と呼び,(2.4)式を用いると
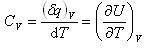 (2.8)
(2.8)
である.*1)
一方,圧力一定の条件で,温度上昇させるときの熱容量を定圧熱容量と呼び,(2.5)式を用いれば
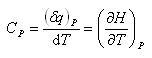 (2.9)
(2.9)
である.
 物質1mol当りの熱容量をモル熱容量といい,1g当りの熱容量を比熱容量という.*2)
物質1mol当りの熱容量をモル熱容量といい,1g当りの熱容量を比熱容量という.*2)
熱容量の測定は熱量計で行う.
すなわち,外界から断熱壁で囲まれた試料容器中の試料に一定の電熱エネルギーを与え,それにともなう物質の温度上昇を測定する.
実験的には,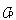 の方が求め易く
の方が求め易く は
は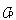 から理論的に定めることができる.
から理論的に定めることができる.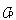 と
と の関係式は,
の関係式は,
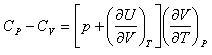 (2.10)
(2.10)
となる.*3)
(2.10)式の第一項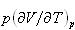 は外圧に抗する膨張の寄与で,第二項
は外圧に抗する膨張の寄与で,第二項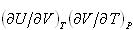 は物質を構成する原子分子同士の凝集力に抗して起こる膨張の寄与である.
は物質を構成する原子分子同士の凝集力に抗して起こる膨張の寄与である.
理想気体では,分子間力はゼロであるから第二項の寄与がゼロ,第一項に理想気体の方程式を代入するとモル熱容量の差は
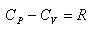 (2.11)
(2.11)
となる.
液体や固体の場合,温度上昇にともなう体積の増加は非常に小さいので,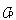 と
と の差は小さい.
の差は小さい.
●気体のモル熱容量
理想気体の分子運動論では,分子間力を無視したので,その内部エネルギーは各分子の運動エネルギーの総和である.
それらは分子間の距離に関係しない.したがって,
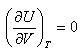 (2.12)
(2.12)
であって,理想気体の内部エネルギーは温度のみの関数である.
それは前章の気体分子運動論で導いたことである.
理想気体では,分子は質点として自由に運動している.それを分子の並進運動と呼ぶ.
第1章で学んだように,分子の運動エネルギーの平均値は,
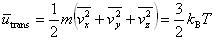 (2.13)
(2.13)
である.
ここで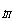 は分子の質量である.
は分子の質量である.
1モルの気体分子の平均運動エネルギーは,アボガドロ定数を掛けて
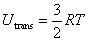 (2.14)
(2.14)
となる.
この結果は,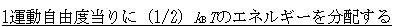 というエネルギー等分配の規則に基づくものである.
というエネルギー等分配の規則に基づくものである.
分子の運動自由度としては,並進運動のほかに分子の重心の周りの回転運動がある.
いま,回転軸のx,y,zの周りの回転の角速度をそれぞれ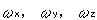 とすると,それぞれの軸の周りの回転エネルギーは,
とすると,それぞれの軸の周りの回転エネルギーは,
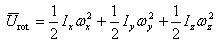 (2.15)
(2.15)
である.
ここで,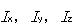 はそれぞれx,y,z軸の周りの慣性モーメントである.
はそれぞれx,y,z軸の周りの慣性モーメントである.
直線分子の場合,分子軸をzとするとz軸の周りの回転運動の寄与はない.
したがって,エネルギー等分配の規則を適用すると,回転運動のエネルギーは1モル当り
 (2.16)
(2.16)
 (2.17)
(2.17)
である.
分子の振動運動のエネルギーを考えよう.
分子には,その構成原子数を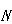 とすると直線分子の場合,
とすると直線分子の場合,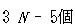 の,非直線分子では
の,非直線分子では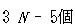 の基準振動が存在する.
の基準振動が存在する.
いま,1番目の基準振動のエネルギーを考えると,それは,換算質量μiの質点の運動量や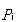 の運動エネルギーと基準座標の微小変位qIにともなうポテンシャルエネルギーの和である.
の運動エネルギーと基準座標の微小変位qIにともなうポテンシャルエネルギーの和である.
したがって,全基準振動のエネルギーは
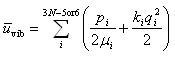 (2.18)
(2.18)
である.
これにエネルギー等分配の規則をあてはめると,基準振動のモード当りの1モル当りのエネルギーは
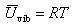 (2.19)
(2.19)
である.
以上の結果より分子の各運動自由度の気体のモル熱容量への寄与を考えると,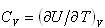 であるから
であるから
 (2.20)
(2.20)
となる.
そこで,表2-1の実験データを調べてみよう.
この表では,定積モル熱容量を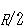 で除した数も与えてあって,モル熱容量に寄与する運動自由度の数を判断し易くする配慮がしてある.
で除した数も与えてあって,モル熱容量に寄与する運動自由度の数を判断し易くする配慮がしてある.
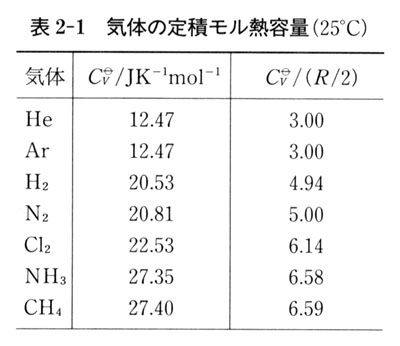 単原子気体の
単原子気体の は
は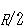 の3倍で,並進運動エネルギーが内部エネルギーである.
の3倍で,並進運動エネルギーが内部エネルギーである.
2原子分子気体では, は
は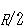 の5倍前後である.
の5倍前後である.
それは,並進と回転運動の両方の寄与を考えると理解できる.
これらの分子には振動運動自由度があるが,エネルギーの等分配規則は当てはまらない.
それは,後に説明するようにエネルギー分配の量子効果のためである.
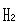 の
の が
が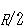 の3倍より小さいのは,回転量子準位の間隔が比較的大きいので,回転運動自由度へのエネルギー等分配が完全に成立していないためである.
の3倍より小さいのは,回転量子準位の間隔が比較的大きいので,回転運動自由度へのエネルギー等分配が完全に成立していないためである.
また,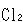 の
の が
が 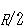 の5倍より大きいのは,その振動量子準位間隔が比較的小さいので,常温でも振動運動自由度ヘエネルギー分配が少し起こるからである.
の5倍より大きいのは,その振動量子準位間隔が比較的小さいので,常温でも振動運動自由度ヘエネルギー分配が少し起こるからである.
多原子分子気体の場合,振動運動を除くと は
は 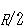 の6倍になるはずである.
の6倍になるはずである.
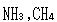 の
の はともに
はともに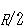 の約6倍となっている.
の約6倍となっている.
熱容量の実験値が分子の運動自由度へのエネルギー等分配の考え方でよく理解できる事実は,熱力学第一法則で定義した内部エネルギーが物質を構成する分子のエネルギーであることを物語っている.
●エネルギー分配の量子効果
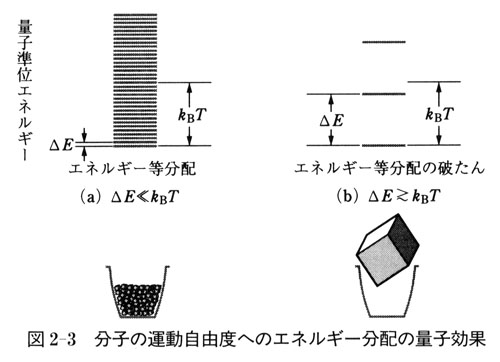
物質のエネルギー状態は基本的に量子準位で表され,とびとびの値である.
図2-3に示すように,準位と準位の間隔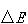 が
が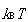 に比べてずっと小さいとき(a)は,
に比べてずっと小さいとき(a)は,
温度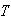 でのその運動自由度へのエネルギー分配に等分配の規則が成立する.
でのその運動自由度へのエネルギー分配に等分配の規則が成立する.
その場合には準位は実質的に連続で,古典力学の考え方が適用できる.
一方,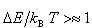 となると(b)等分配の規則は成立せずそれよりずっと少ないエネルギーしか分配されない.
となると(b)等分配の規則は成立せずそれよりずっと少ないエネルギーしか分配されない.
したがって,モル熱容量は等分配規則で予測するよりも小さくなる.量子準位の分布については,第4章で改めて詳しく触れるが,図2-3に量子効果をわかり易く説明した図がある.
温度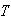 の物質の状態は,
の物質の状態は,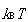 という容積をもつ容器が量子エネルギーを受け取る仕方で定まる.
という容積をもつ容器が量子エネルギーを受け取る仕方で定まる.
量子エネルギーの単位が小さいときは,容器に量子エネルギーの単位をどのようにもつめることができる.
一方,量子エネルギーの単位が大きいと容器の中に入らなくなる.容器の大きさは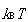 で,いま,
で,いま,
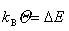 (2.21)
(2.21)
となる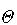 を特性温度と呼ぶ.
を特性温度と呼ぶ.
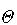 が高いと高い温度で量子効果が現れる.
が高いと高い温度で量子効果が現れる.
●固体のモル熱容量
結晶を構成する原子は,x,y,zの3方向に沿って振動運動をする.
したがって,結晶内の原子の振動に対してエネルギー等分配の規則を適用すると,三つのモードにそれぞれ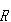 の熱容量の寄与があるから,結晶のモル熱容量は3
の熱容量の寄与があるから,結晶のモル熱容量は3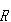 になるはずである.
になるはずである.
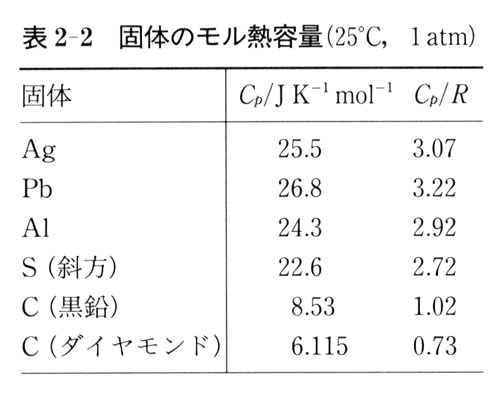
表2-2によれば,多くの金属のモル熱容量は約25JK-1mol-1となっている.
この傾向は,デューロン-プティー(Dulong-Petit)の経験則として知られている.
ダイヤモンド結晶のモル熱容量は,3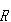 よりもはるかに小さい.
よりもはるかに小さい.
それは,ダイヤモンドを構成する炭素原子間の結合が強く,その振動数が高く,特性温度が高いからである.
結晶の熱容景の理論を提唱したデバイ(P. Debye)の名を冠して,結晶の特性温度をデバイ温度という.
図2-4に結晶のモル熱容量の温度依存性を示した.
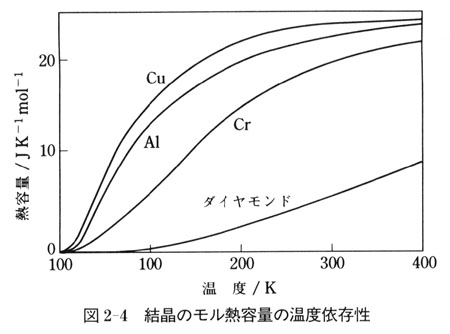
常温付近で3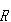 のモル熱容量をもつ結晶も低温になると
のモル熱容量をもつ結晶も低温になると が小さくなり,0Kの極限では
が小さくなり,0Kの極限では = 0となる.
= 0となる.
 は温度を1 Kだけ上昇させるのに必要な熱エネルギーであるからそれが0というのは意外に思われる.
は温度を1 Kだけ上昇させるのに必要な熱エネルギーであるからそれが0というのは意外に思われる.
これは物質のエネルギーは量子準位への分布であると考えると説明できる.
0Kは到達できない温度であるが,そこでは最低の準位にすべての分子が分布している.
次の量子準位は,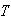 = 0の極限では
= 0の極限では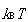 よりはるかに高い準位にある.
よりはるかに高い準位にある.
そのため,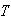 → 0の極限で熱容景はゼロとなる.このことは,第4章の熱力学第二法則の項で再びとり上げる.
→ 0の極限で熱容景はゼロとなる.このことは,第4章の熱力学第二法則の項で再びとり上げる.
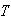 から
から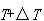 に上昇させるとき系が外界から吸収する熱を
に上昇させるとき系が外界から吸収する熱を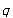 とする.
とする.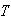 において,系の温度を単位だけ上昇させるのに必要な熱を熱容量と呼び,次のように定義される.
において,系の温度を単位だけ上昇させるのに必要な熱を熱容量と呼び,次のように定義される.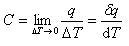 (2.7)
(2.7)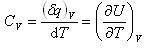 (2.8)
(2.8)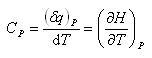 (2.9)
(2.9) 物質1mol当りの熱容量をモル熱容量といい,1g当りの熱容量を比熱容量という.*2)
物質1mol当りの熱容量をモル熱容量といい,1g当りの熱容量を比熱容量という.*2)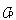 の方が求め易く
の方が求め易く は
は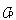 から理論的に定めることができる.
から理論的に定めることができる.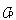 と
と の関係式は,
の関係式は,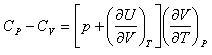 (2.10)
(2.10)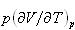 は外圧に抗する膨張の寄与で,第二項
は外圧に抗する膨張の寄与で,第二項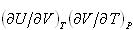 は物質を構成する原子分子同士の凝集力に抗して起こる膨張の寄与である.
は物質を構成する原子分子同士の凝集力に抗して起こる膨張の寄与である.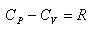 (2.11)
(2.11)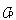 と
と の差は小さい.
の差は小さい.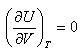 (2.12)
(2.12)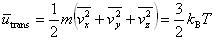 (2.13)
(2.13)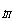 は分子の質量である.
は分子の質量である.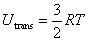 (2.14)
(2.14)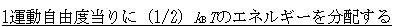 というエネルギー等分配の規則に基づくものである.
というエネルギー等分配の規則に基づくものである.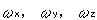 とすると,それぞれの軸の周りの回転エネルギーは,
とすると,それぞれの軸の周りの回転エネルギーは,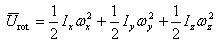 (2.15)
(2.15)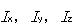 はそれぞれx,y,z軸の周りの慣性モーメントである.
はそれぞれx,y,z軸の周りの慣性モーメントである. (2.16)
(2.16) (2.17)
(2.17)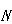 とすると直線分子の場合,
とすると直線分子の場合,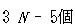 の,非直線分子では
の,非直線分子では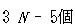 の基準振動が存在する.
の基準振動が存在する.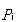 の運動エネルギーと基準座標の微小変位qIにともなうポテンシャルエネルギーの和である.
の運動エネルギーと基準座標の微小変位qIにともなうポテンシャルエネルギーの和である.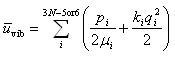 (2.18)
(2.18)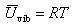 (2.19)
(2.19)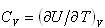 であるから
であるから (2.20)
(2.20)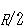 で除した数も与えてあって,モル熱容量に寄与する運動自由度の数を判断し易くする配慮がしてある.
で除した数も与えてあって,モル熱容量に寄与する運動自由度の数を判断し易くする配慮がしてある. 単原子気体の
単原子気体の は
は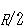 の3倍で,並進運動エネルギーが内部エネルギーである.
の3倍で,並進運動エネルギーが内部エネルギーである. は
は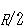 の5倍前後である.
の5倍前後である.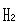 の
の が
が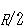 の3倍より小さいのは,回転量子準位の間隔が比較的大きいので,回転運動自由度へのエネルギー等分配が完全に成立していないためである.
の3倍より小さいのは,回転量子準位の間隔が比較的大きいので,回転運動自由度へのエネルギー等分配が完全に成立していないためである.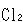 の
の が
が 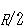 の5倍より大きいのは,その振動量子準位間隔が比較的小さいので,常温でも振動運動自由度ヘエネルギー分配が少し起こるからである.
の5倍より大きいのは,その振動量子準位間隔が比較的小さいので,常温でも振動運動自由度ヘエネルギー分配が少し起こるからである. は
は 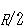 の6倍になるはずである.
の6倍になるはずである.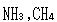 の
の はともに
はともに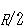 の約6倍となっている.
の約6倍となっている.
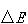 が
が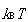 に比べてずっと小さいとき(a)は,
に比べてずっと小さいとき(a)は,
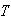 でのその運動自由度へのエネルギー分配に等分配の規則が成立する.
でのその運動自由度へのエネルギー分配に等分配の規則が成立する.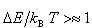 となると(b)等分配の規則は成立せずそれよりずっと少ないエネルギーしか分配されない.
となると(b)等分配の規則は成立せずそれよりずっと少ないエネルギーしか分配されない.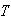 の物質の状態は,
の物質の状態は,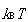 という容積をもつ容器が量子エネルギーを受け取る仕方で定まる.
という容積をもつ容器が量子エネルギーを受け取る仕方で定まる.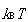 で,いま,
で,いま,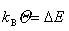 (2.21)
(2.21)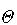 を特性温度と呼ぶ.
を特性温度と呼ぶ.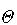 が高いと高い温度で量子効果が現れる.
が高いと高い温度で量子効果が現れる.
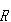 の熱容量の寄与があるから,結晶のモル熱容量は3
の熱容量の寄与があるから,結晶のモル熱容量は3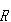 になるはずである.
になるはずである.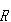 よりもはるかに小さい.
よりもはるかに小さい.
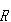 のモル熱容量をもつ結晶も低温になると
のモル熱容量をもつ結晶も低温になると が小さくなり,0Kの極限では
が小さくなり,0Kの極限では = 0となる.
= 0となる. は温度を1 Kだけ上昇させるのに必要な熱エネルギーであるからそれが0というのは意外に思われる.
は温度を1 Kだけ上昇させるのに必要な熱エネルギーであるからそれが0というのは意外に思われる.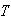 = 0の極限では
= 0の極限では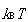 よりはるかに高い準位にある.
よりはるかに高い準位にある.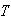 → 0の極限で熱容景はゼロとなる.このことは,第4章の熱力学第二法則の項で再びとり上げる.
→ 0の極限で熱容景はゼロとなる.このことは,第4章の熱力学第二法則の項で再びとり上げる.