3.物質のエントロピー
●標準エントロピー
標準状態において物質のエントロピーを実験的に求めることができる.
それには,標準状態でのモル熱容量や転移温度,転移エンタルピーのデータが必要である.
純物質を0 Kから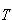 Kに加熱する際のエントロピーの増加は,途中で起こる相転移を考えに入れると,
Kに加熱する際のエントロピーの増加は,途中で起こる相転移を考えに入れると,
 (4.13)
(4.13)
となる.
これは,(3.2)式の標準エンタルピーの定義に対応するものである.
主な物質についての標準エントロピーの値は,付録3に与えてある.
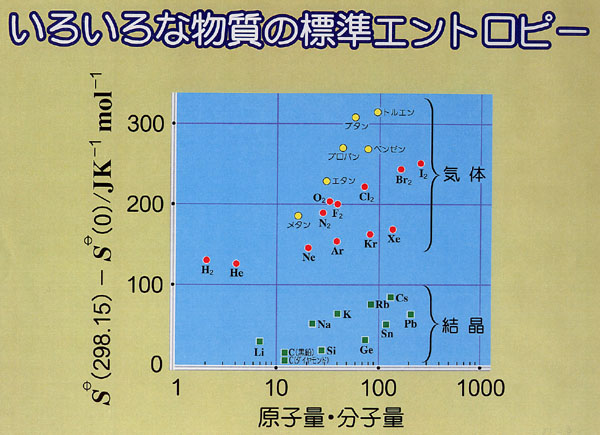
●熱力学第三法則
ネルンスト(W.H.Nernst)は実験事実より「純粋な固体物質の等温等圧の下での物理的また化学的変化において,エントロピーの変化は絶対温度とともに零に近付く」という定理を提唱した.
この定理は,プランクによって発展されて「純物質の完全結晶のエントロピーは絶対零度で0である」とされた.**)
**)この定理の別のいい方に「いかなる方法によっても有限回の操作で系の温度を絶対零度に下げることはできない」がある.それは,絶対零度への到達不可能の原理を述べたものである.
これは,熱力学第三法則と呼ばれることもある.
第三法則をボルツマンの原理で解釈すると,絶対零度の極限状態では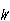 = 1となる.
= 1となる.
つまり,絶対零度では,系に許される量子準位はただ一つでなければならない.
●残余エントロピー
ボルツマンの原理で定義されたエントロピーは分配関数を計算することによって理論的に求めることができる.
そのようなことが厳密にできるのは,理想気体の分子についてである.
計算のためには,分子の回転や振動の分光データから量子準位エネルギー値が必要である.
表4-1にいくつかの物質の実験で求められたエントロピー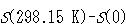 と分光データに基づいた計算値
と分光データに基づいた計算値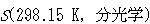 とが比較してある.
とが比較してある.
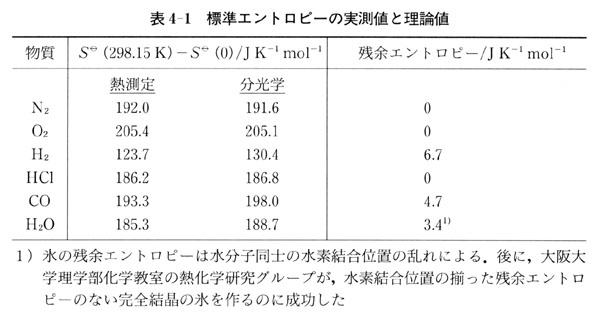
二つのエントロピーがよく一致しているものもあるが,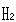 ,
,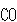 と
と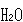 については,実験値の方が計算値よりも小さく,
については,実験値の方が計算値よりも小さく,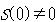 が結論される.
が結論される.
これは熱力学第三法則に反するものではない.
それらの物質が絶対零度において完全な結晶でなく,構造に「無秩序さ」が残っていることを意味している.
その意味で,ここで求められたみかけの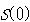 を残余エントロピーという.
を残余エントロピーという.
有限な残余エントロピーが観測された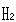 では,H原子核のスピンの配列がそろったオルト
では,H原子核のスピンの配列がそろったオルト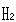 と反平行のパラ
と反平行のパラ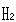 の間の平衡が凍結されたまま,極低温の固体になる.
の間の平衡が凍結されたまま,極低温の固体になる.
オルト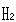 の全核スピンは1で,パラ
の全核スピンは1で,パラ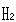 のそれは0である.
のそれは0である.
したがって,その統計的重率は3:1の比率となる.
オルト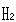 がパラ
がパラ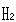 へ変換せずに
へ変換せずに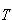 → 0の固体となると,
→ 0の固体となると,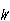 = 3の無秩序さが残ることになる.
= 3の無秩序さが残ることになる.
つまり,3/4の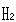 が
が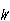 = 3をとる.
= 3をとる.
したがって,残余エントロピーの理論値は,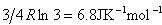 となり,実験値をよく説明する.
となり,実験値をよく説明する.
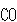 の場合は,結晶内で
の場合は,結晶内で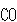 の分子配向に乱れのある結晶がそのまま極低温に冷却されるためとされている.
の分子配向に乱れのある結晶がそのまま極低温に冷却されるためとされている.
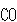 の方向に2通りあるから
の方向に2通りあるから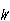 = 2である.
= 2である.
すると,残余エントロピーは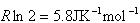 となる.
となる.
実験値より少し大きい見積りであるが,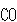 の結晶が不完全であると結論してよい.
の結晶が不完全であると結論してよい.
最後の氷の不完全さについては,二つの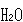 分子にはさまれたH原子の位置に二つの場所が可能で,その位置が乱れた不完全な氷のまま極低温となるためとされている.
分子にはさまれたH原子の位置に二つの場所が可能で,その位置が乱れた不完全な氷のまま極低温となるためとされている.
それについては,問題3で残余エントロピーの計算をして頂くよう配慮した.
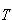 Kに加熱する際のエントロピーの増加は,途中で起こる相転移を考えに入れると,
Kに加熱する際のエントロピーの増加は,途中で起こる相転移を考えに入れると, (4.13)
(4.13)
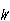 = 1となる.
= 1となる.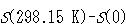 と分光データに基づいた計算値
と分光データに基づいた計算値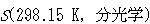 とが比較してある.
とが比較してある.
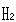 ,
,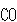 と
と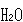 については,実験値の方が計算値よりも小さく,
については,実験値の方が計算値よりも小さく,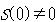 が結論される.
が結論される.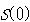 を残余エントロピーという.
を残余エントロピーという.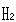 では,H原子核のスピンの配列がそろったオルト
では,H原子核のスピンの配列がそろったオルト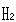 と反平行のパラ
と反平行のパラ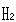 の間の平衡が凍結されたまま,極低温の固体になる.
の間の平衡が凍結されたまま,極低温の固体になる.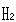 の全核スピンは1で,パラ
の全核スピンは1で,パラ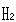 のそれは0である.
のそれは0である.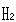 がパラ
がパラ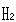 へ変換せずに
へ変換せずに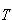 → 0の固体となると,
→ 0の固体となると,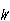 = 3の無秩序さが残ることになる.
= 3の無秩序さが残ることになる.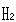 が
が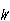 = 3をとる.
= 3をとる.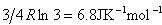 となり,実験値をよく説明する.
となり,実験値をよく説明する.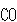 の場合は,結晶内で
の場合は,結晶内で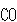 の分子配向に乱れのある結晶がそのまま極低温に冷却されるためとされている.
の分子配向に乱れのある結晶がそのまま極低温に冷却されるためとされている.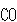 の方向に2通りあるから
の方向に2通りあるから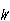 = 2である.
= 2である.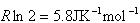 となる.
となる.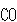 の結晶が不完全であると結論してよい.
の結晶が不完全であると結論してよい.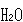 分子にはさまれたH原子の位置に二つの場所が可能で,その位置が乱れた不完全な氷のまま極低温となるためとされている.
分子にはさまれたH原子の位置に二つの場所が可能で,その位置が乱れた不完全な氷のまま極低温となるためとされている.