5.理想希薄溶液
ラウールの法則を満たさない溶液においても小さい濃度の領域で理想溶液と見倣すことができる.
すなわち,図7-2(b)や(c)の溶液でも十分希薄な条件下で化学ポテンシャルを
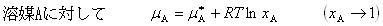 (7.11)
(7.11)
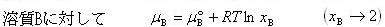 (7.12)
(7.12)
である.
ここで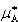 純溶媒の化学ポテンシャルである.
純溶媒の化学ポテンシャルである.
しかし,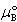 は(7.12)式が
は(7.12)式が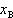 =1でも成立すると仮定したときの溶質の化学ポテンシャルで,純粋なB物質の化学ポテンシャルではない.
=1でも成立すると仮定したときの溶質の化学ポテンシャルで,純粋なB物質の化学ポテンシャルではない.
●蒸気圧降下・沸点上昇・凝固点降下
溶液の蒸気圧と溶媒のそれとを比較した相対的な低下の度合を平衡の条件から導くことができる.
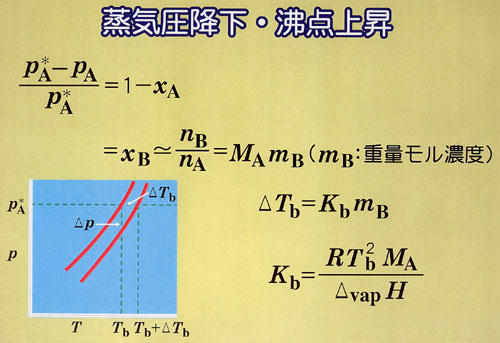
すなわち,溶媒Aの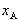 →1の条件において
→1の条件において
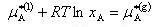 (7.13)
(7.13)
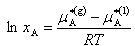 (7.14)
(7.14)
となる.
この式を圧力一定でTについて微分し,付録7の中の熱力学関係式の中のギブズ−ヘルムホルツの式を用いると,
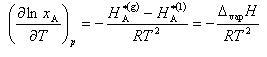 (7.15)
(7.15)
が得られる.
ここで,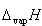 は溶媒の蒸発エンタルピーである.
は溶媒の蒸発エンタルピーである.
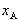 =1の場合,1 atm下では沸点Tbにおいて溶媒の液相と気相は平衡にある.
=1の場合,1 atm下では沸点Tbにおいて溶媒の液相と気相は平衡にある.
いま,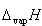 の温度依存性を無視して(7.15)式を
の温度依存性を無視して(7.15)式を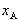 =1から
=1から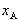 まで,また,TbからTまで積分する.
まで,また,TbからTまで積分する.
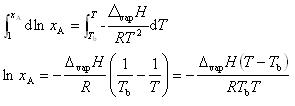
いま,沸点上昇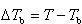 ,
,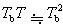 ,
,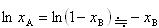 とすれば
とすれば
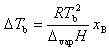
を得る.
いま,Bの質量モル濃度を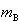 とすると
とすると
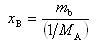
である.
ここで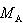 は溶媒のkg単位のモル質量である.
は溶媒のkg単位のモル質量である.
すると
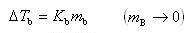 (7.16)
(7.16)
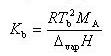 (7.17)
(7.17)
を得る.
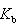 はモル沸点上昇定数である.
はモル沸点上昇定数である.
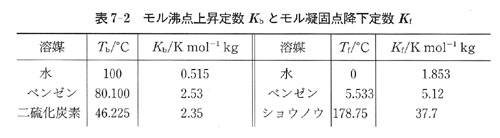
圧力一定下で溶液を冷却したとき固相が析出する温度は凝固点である.
図7-9や図7-10に示したように析出する固相が純溶媒の固体の場合,溶液の凝固点は溶媒の凝固点よりも低い.
溶媒の凝固点と溶液の凝固点の差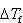 を凝固点降下という.
を凝固点降下という.
理想希薄溶液の凝固点降下は溶質の質量モル濃度に比例する.
 (7.18)
(7.18)
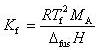 (7.19)
(7.19)
ここで,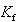 はモル凝固点降下定数と呼ばれ,沸点上昇の場合と同じように化学ポテンシャルから求めることができる.
はモル凝固点降下定数と呼ばれ,沸点上昇の場合と同じように化学ポテンシャルから求めることができる.
●浸透圧

溶液と溶媒が溶媒分子だけを透過させる半透膜を隔てて存在すると,溶媒は膜を通って溶液中へ拡散しようとする.
これを阻止して溶液と溶媒の間の平衡を保つには図7-12に示すように溶液に余分の圧力を加える必要がある.これを浸透圧という.
ファントホッフはショ糖水溶液の浸透圧を溶質のモル濃度や温度の関数で測定し,次のファントホッフの式を得た.
 (7.20)
(7.20)
この式は,半透膜で隔てられた溶媒Aと溶液中の溶媒の化学ポテンシャルが平衡している条件から求めることができる.
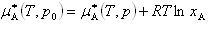 (7.21)
(7.21)
ここで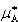 は純溶媒の化学ポテンシャルであるからその圧力変化は
は純溶媒の化学ポテンシャルであるからその圧力変化は
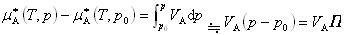
となる.
ただし,溶媒Aのモル体積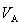 は圧力によって変化しないとした.(7.21)式より
は圧力によって変化しないとした.(7.21)式より
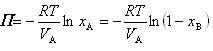 (7.22)
(7.22)
が得られる.
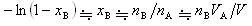 (Vは溶液の体積)であるから(7.22)式は
(Vは溶液の体積)であるから(7.22)式は
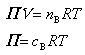 (7.23)
(7.23)
に帰着する.
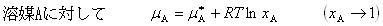 (7.11)
(7.11)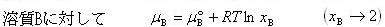 (7.12)
(7.12)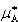 純溶媒の化学ポテンシャルである.
純溶媒の化学ポテンシャルである.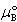 は(7.12)式が
は(7.12)式が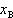 =1でも成立すると仮定したときの溶質の化学ポテンシャルで,純粋なB物質の化学ポテンシャルではない.
=1でも成立すると仮定したときの溶質の化学ポテンシャルで,純粋なB物質の化学ポテンシャルではない.
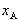 →1の条件において
→1の条件において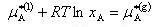 (7.13)
(7.13)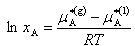 (7.14)
(7.14)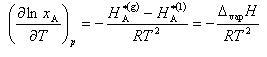 (7.15)
(7.15)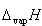 は溶媒の蒸発エンタルピーである.
は溶媒の蒸発エンタルピーである.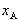 =1の場合,1 atm下では沸点Tbにおいて溶媒の液相と気相は平衡にある.
=1の場合,1 atm下では沸点Tbにおいて溶媒の液相と気相は平衡にある.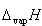 の温度依存性を無視して(7.15)式を
の温度依存性を無視して(7.15)式を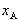 =1から
=1から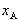 まで,また,TbからTまで積分する.
まで,また,TbからTまで積分する.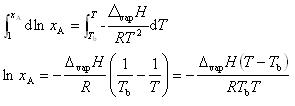
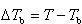 ,
,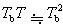 ,
,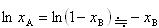 とすれば
とすれば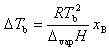
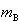 とすると
とすると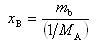
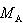 は溶媒のkg単位のモル質量である.
は溶媒のkg単位のモル質量である.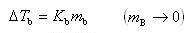 (7.16)
(7.16)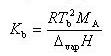 (7.17)
(7.17)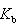 はモル沸点上昇定数である.
はモル沸点上昇定数である.
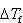 を凝固点降下という.
を凝固点降下という. (7.18)
(7.18)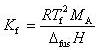 (7.19)
(7.19)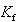 はモル凝固点降下定数と呼ばれ,沸点上昇の場合と同じように化学ポテンシャルから求めることができる.
はモル凝固点降下定数と呼ばれ,沸点上昇の場合と同じように化学ポテンシャルから求めることができる.
 (7.20)
(7.20)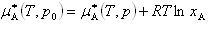 (7.21)
(7.21)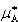 は純溶媒の化学ポテンシャルであるからその圧力変化は
は純溶媒の化学ポテンシャルであるからその圧力変化は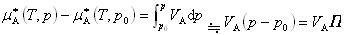
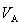 は圧力によって変化しないとした.(7.21)式より
は圧力によって変化しないとした.(7.21)式より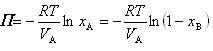 (7.22)
(7.22)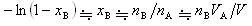 (Vは溶液の体積)であるから(7.22)式は
(Vは溶液の体積)であるから(7.22)式は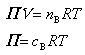 (7.23)
(7.23)