第2章 分子の形成
種々の元素の原子は星の中における原子核反応の結果生まれるが,生まれた時は単原子状態にあると考えられている。
原子からは各種の分子が生成し,星と星の間の星間空間には多種類の分子が観測される。
それらは地球に存在する物も存在しない物もある。
分子の形成は原子から複雑な物質系が生まれる第一歩である。
分子には希ガス分子のように単原子からなる物もあるが,多くは2原子以上の集まりであり,3原子以上になると色々の形をとる。
本回では原子間特に非金属元素の原子間に働く共有結合についてその近似方法を考え,結合の結果生まれた分子の最も基本的性質を学ぶ。
1.共有結合の近似
非金属元素の原子どうしが作る分子は,電子が関係原子間に共有されると考えて説明できる。
共有結合は色々に近似できるが,比較的分かりやすく詳細な近似にも役立つのがLCAO法(Linear Combination of Atomic Orbitals)という方法である。
これは分子を作る原子それぞれの状態を示す波動方程式の一次結合によって分子の電子状態を表現するところから名付けられた。
(1)同種原子間のLCAO
図2-1(a),(b)に水素分子を例として同種原子の共有結合を粗い近似で示した。
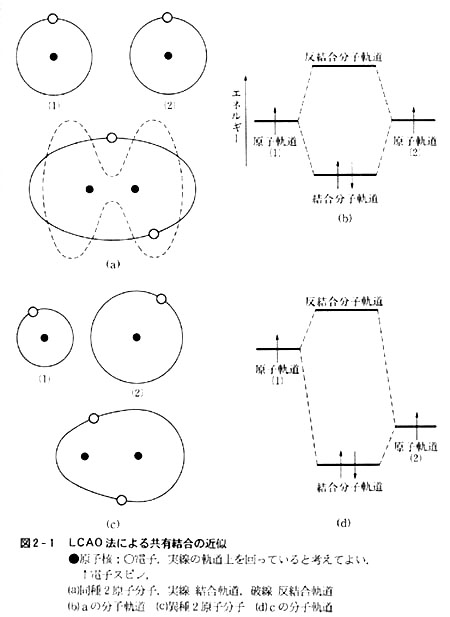
共有結合を作る以前には,原子(1)の電子は原子(1)の原子核とだけ,原子(2)の電子は原子(2)の原子核とだけ相互作用を持っていたが,2原子分子の生成によって,どちらの電子も両方の原子核と均等に相互作用するようになる。
2個の電子は電子対を作って,スピン量子数が正負打ち消すようになっている。このことは生じた水素分子が反磁性であることから証明される。(水素の単原子は不対電子をもち常磁性である。)
共有された電子は両原子の中間に存在確率が大きい。
これをエネルギーレベルにして書くと図2-1(b)のようになり,原子の電子軌道(原子軌道と呼ぶ)よりエネルギーの低い新しい軌道に共有された電子が入るが,この軌道を結合分子軌道(略して結合軌道)という。
この時同時にもとの原子軌道よりもエネルギーの高い軌道―反結合分子軌道―をも生じる。この軌道には電子は通常の状態では存在しない。その形は図の通りで,両原子の中間には存在確率が少ない。
分子がエネルギーを与えられたり,化学反応を起こすときには重要な役割を果たす。
一般に,一つの電子軌道にはスピン量子数の異なる2個の電子を収容することが可能で,その2電子はスピンが逆向きになり,反磁性を示す。
水素原子に限らず,ハロゲン元素の原子が作る2原子分子にも同様にLCAO法を適用できる。
この時は原子の結合軸をz方向にとり,原子軌道は2pzどうしを組み合わせる。
酸素や窒素の分子には2重結合および3重結合を考える必要があり,第3回で扱う。
(2)異種原子間のLCAO
共有結合を作る原子の種類が異なる場合のLCAOの例を図2-1の(c)(d)に示した。
原子(1)および原子(2)の結合にあずかる電子は両方の原子核と相互作用を持つが,同種原子間の場合と違って両原子と均等にではなく,一方の原子核とより多くの相互作用を持つ。このことは,一方の原子核の影響を受けている時間の方が長いといってもよい。
この分子軌道の状態を(d)に示す。
2種の原子のうちエネルギーの低い方を原子(2)とするが,これはイオン化エネルギーの高い方の原子だと考えればまず誤りはない。
フッ化水素HFならFが(2)となり,(b)の場合と同様,結合軌道と反結合軌道を画くことができる。
エネルギーレベルについても形についても,前者は原子(2)の原子軌道に,後者は原子(1)の原子軌道に近い。
つまりフッ化水素の結合分子軌道はフッ素のそれに近く,Fの原子核から,より大きい影響を受けることになる。
分子軌道を考える時原子(1)と原子(2)のどんな軌道でも任意に組み合わせてよいわけではなく,一定の制約がある。
この制約は原子軌道を示す波動方程式の対称性と関係がある。
詳しいことは専門科目「物質の科学Ⅱ」で扱われるが,一つの条件は同方向に広がる軌道どうしに限られる点である。
2原子分子の結合軸をzにとれば,pzとpzの組み合わせは可能だが,pxとpzの組み合わせは許されない。(このほか原子軌道が対称中心を持つgか,持たないuかも重要な条件であるが省略する。)
分子内で電子の存在が原子(2)の側に偏ることによって,分子内での電子分布は均等でなくなり,分子全体として電気的な正負が現れる。
これは分子としての重要な性質の一つで,双極子モーメントと呼ばれる。
(3)3原子以上の場合
水H2O(V字型),アンモニアNH3(三角錐),メタンCH4(正四面体)のような多原子分子は一定の形を持つが,分子型は気体の電子線回折,固体のX線回折などの方法で実験的に決定できる。
分子中の共有結合はやはりLCAO法で近似する。いくら構成原子数が多くなっても共有結合は2原子の間で考えるという点が重要である。
水ではO-H結合を2つ,アンモニアではN-Hを3つ,メタンではC-Hを4つ考える。(希な例として3中心2電子結合がある。第3回。)
その一つ一つについては図2-1(c)(d)のような近似を行うが,LCAOを適用しうる条件を満たすためには,原子軌道に変更を加える必要がある。
(4)軌道の混成
メタンは正四面体を持ち,C-H間隔は1.087Å,∠HCHは109°28′(正四面体の中心から頂点をみる角)が測定されている。
炭素原子の持つ1s2s2pの電子軌道には,この方向に向いた物はない。
そこで外側にある2s軌道と3本の2p軌道を組み替えて,正四面体の頂点方向に向く4本の軌道を作りだす。
これは各軌道を表現する波動方程式の操作で行う。このような操作を軌道の混成といい,メタンの場合はs軌道1本とp軌道3本を混成したのでsp3混成という。
ここで生じた4本の混成軌道をh1,h2,h3,h4のように示す。
どの軌道でも任意に混成してよいのではなく,一定の制約がある。
しばしば用いられる混成軌道を表2-1に示した。

メタンの分子軌道を考える際には,基底状態にある炭素原子の2s22p2の4個の電子をh1~h4軌道に1個ずつ配置してh11h21h31h41の状態とし,この一つと水素原子の1s1との間にLCAO法を適用すればよい。
炭素原子の基底状態は2s22p2の電子配置だから,これをh11h21h31h41に変えるにはエネルギーを加える必要がある。
この意味で混成軌道に電子を配置した状態は一種の励起状態である。
分子軌道を考えるための準備として考えた励起状態を原子価状態という。(フッ素水素のように,原子価状態を考えずに基底状態から分子軌道を作り上げることも可能である。)
アンモニアの場合もsp3混成を考えるが,窒素原子は基底状態で2s22p3配置をとっており,(化学結合に関係しない1s軌道は省略),5個の電子をh1~h4軌道に配置した原子価状態はh11h21h31h42となり,このうちh1~h3が水素原子と結合する。h4軌道は結合に関与せず,非結合軌道と呼ばれ,その電子対は非結合電子対(略して非結合対,孤立対ともいう)という。
非結合対はアンモニア分子が他のイオンや分子と相互作用する時重要な役割を果たす。水分子は2対の非結合対を持つ。

