2.分子レベルの性質
分子からなる物質の性質には,分子そのものの性質と(表2-2),分子が集まり液体や固体―分子集団―を作った時の性質とがある(密度,融点,沸点など,第4回)。

分子レベルの性質でも単分子での測定は不可能で,多数の分子を用いて測定する。
分子レベルの性質のうち結合の強さ以外の量は直接測定が可能である。
(1) 磁性
物質を磁場(例えば磁石の近く)に近づけた時,磁場の強い方へ引っ張られる物と,弱い方へ反発される物とがある。
前者を常磁性物質,後者を反磁性物質といい,その程度を磁化率という。磁化率は真空の磁化率との比をとり,体積当り,質量当り,またはモル当りで示す。
反磁性は負の値となる。常磁性は,磁化率の温度変化に基づいてさらに分類が可能である。(第11,14回)
常磁性の原因は対になっていない電子(不対電子)にある。一方対電子は結合対,非結合対ともに反磁性の原因となる。
しかしその程度(反磁性磁化率)は常磁性磁化率にくらべ絶対値が1桁小さい。
それゆえ,反磁性は不対電子が存在しない証拠となる。
非金属元素の作る分子性物質は大部分が反磁性である。
常磁性を示す例は極めて少なく,電子総数が奇数のNO,NO2および有機の遊離基,さらに電子総数は偶数なのに強い常磁性を示す酸素分子に限られる。
一方遷移元素化合物とくに錯体には,電子総数が偶数でも常磁性を示すものが多い。
(2)双極子モーメン卜
分子中における電荷の偏りを示すのが双極子モーメン卜である。
分子を電場の中に置くと(図2-2),分子中の電子は正電荷に引かれて偏りを示す。
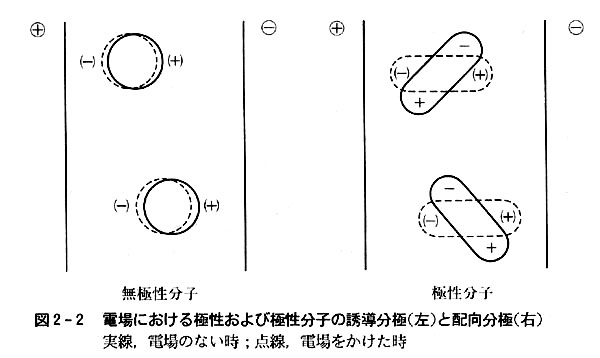
このような偏りを誘起効果といい,生じた電荷の偏りを誘起双極子という。
どんな分子でも多少の差はあるが誘起を生じる。
分子自身に電荷の偏りがあると電場に置かれた時,誘起効果のほかに,分子自身の持つ電荷の偏り(永久双極子という)が電場の方向と反対に向くように分子が向きを変える。
これを配向効果という。
永久双極子を持つ分子を極性分子,持たないものを無極性分子という。
極性分子中の電荷の偏りの程度(双極子モーメントμ)は(電気量×長さ)の次元を持ち,通常はデバイ(D,1D=3.33×10-30Cm,Cはクーロン)を単位として示す。
双極子モーメントの測定には,マイク口波領域(波長約1m以下)の電波吸収が電場に置かれた時の変化―波長のずれや吸収の分裂,シュタルク効果という―を観測し,その効果を解析する。
シュタルク効果の観測からは,そのほか傘形分子の反転や,分子の内部回転(第3回)についての情報も得られる。(図2-3,装置などは映像でみる)
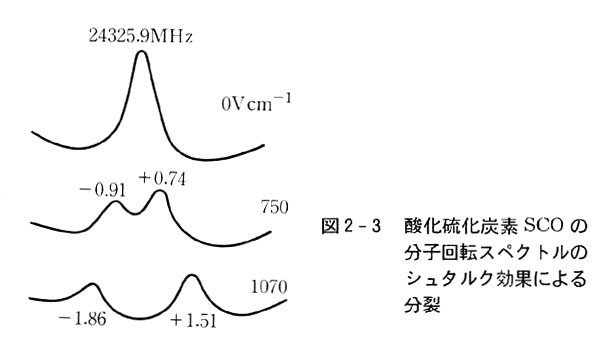
表2-3には簡単な分子のμ値を示した。

2原子分子については,電気陰性度の大きい原子の方が負極になることが多い。
その程度は電気陰性度の差が大きいほど大きい。(ハロゲン化水素,ハロゲン化メチルなど)
これらは共有結合での電子の偏りと分子全体の双極子モーメン卜とが一致する場合である。
これに対し,二酸化炭素OCOのように,各C-O結合にはC+O−のような極性があるが,分子としては相殺して無極性になることもある。
BF3のような正三角形分子も同様である。
これに対し,一酸化炭素,一硫化炭素は顕著な例外である。
結合の極性としてはC+O−が期待されるが,実際の極性はC−O+である。
これは非結合電子対の形によって説明される。
炭素原子はsp混成を持ち,原子価状態ではh21h22px1py0となって,h1がO原子のpz1と通常の共有結合(σ結合)を作り,混成に参加しないpx1py0は,O原子のpx2py1とπ結合を作ったと考える。
酸素原子は混成を生じないで,2s2の非結合対はO原子核に近い所にあるのに,炭素原子上の非結合対h22はO原子と反対の方向に延びてC原子側を負にすると考える。
C上の非結合対は,一酸化炭素が配位子となって有機金属錯体を作る時重要な役割を果たす。
(2) 分極率
分子が電場に置かれた時,全体がどの程度変形しやすいかを示す尺度が分極率である。
誘起効果の起こしやすさの程度といってもよい。
原子核は変形しないから,変形するのは電子の分布状態(電子雲)である。
分極率は体積の次元を持ち,通常10-25m3単位で示す。
分極率は方向によって差があり,2原子分子でも結合軸方向とそれに直角の方向とでは値が異なる。
方向を平均した分極率の値αはローレンツ-ローレンスの式(2.1)を用いて屈折率nから求められる。
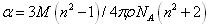 (2.1)
(2.1)
Mは分子量,ρは密度,NAはアボガドロ定数である。
(式(2.1)のn2の代わりに誘電率εを代入したクラウジウス-モソッティの式を用いて,εの測定値から求めることもできる。)
図2-4には液体の屈折率を計るアッベ屈折計の構造を示した。
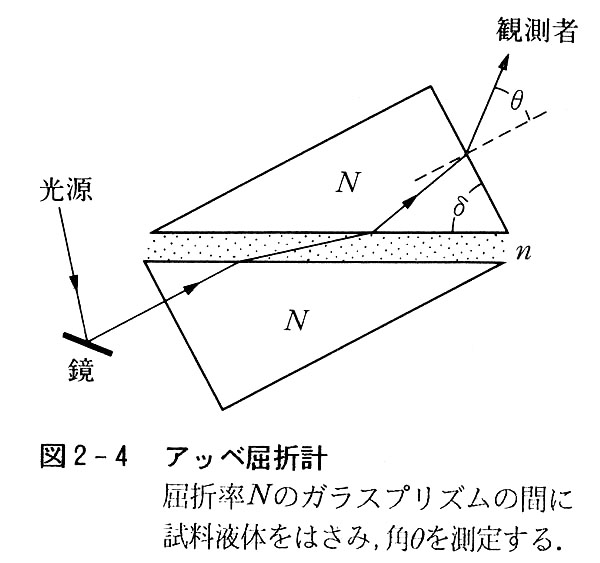
光源と観測者との角度の関係を図のようにとると,式(2.2)が成立する。
 (2.2)
(2.2)
Nとδは装置できまる定数だから,θを測定すればnが求められる。色々の方向における分極率を求めるには光の散乱など複雑な方法を用いる必要がある。
表2-4には2,3の分子の分極率を示した。
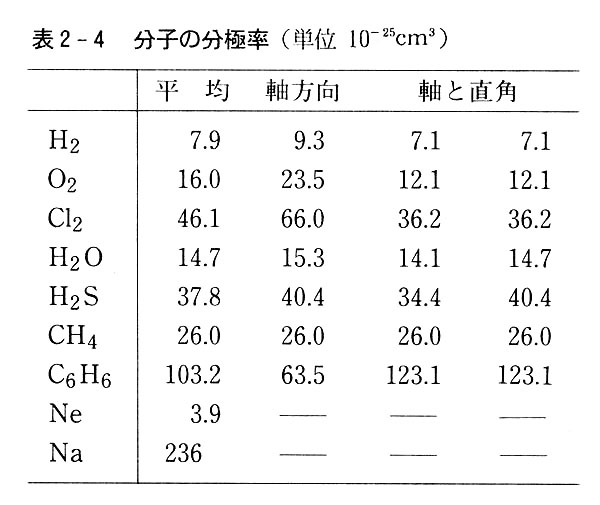
同じような形の分子では大きい分子のα値が大きい。
対称性の高いメタンなどは方向によってαは変化しない。
一般に結合軸方向ではそれと直角の方向よりαが大きい。
分極率は双極子モーメントとともに,分子どうしの間で働く力の大きさを支配する因子となる。(第4回)
(3) イオン化エネルギー
分子のイオン化エネルギーとは分子から電子1個を取り去って陽イオンを生じるのに必要なエネルギーである。
例えばメタンでは, CH4→CH4++e− 12.65eV
のようになる。
測定方法は第6回に映像を用いて説明する。
分子のイオン化エネルギーは原子と違って種類による差が少なく,大部分は8〜13eVの値を持ち,16eVを超えるものは希である。
生じた陽イオンはもとの分子とはいくらか異なる形を持つことが多い。




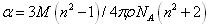 (2.1)
(2.1)
 (2.2)
(2.2)