3.金属結合
金属では原子から固体結晶を生じる中間に「分子」が存在しない。
しいていえば1結晶が1分子ということになる。
2.で述べた金属の物性を説明するためには,金属に独特な結合状態―金属結合―を考える必要がある。
(1)近似の方法
大部分の金属は最密構造をとり,配位数は8または12である。
代表としてナトリウムのようなアルカリ金属(体心立方格子,A2型)を考えると,各原子は希ガス型に電子1個が加わった電子配置を持ち,結合に関与しうる電子は原子当り1個である。
Na原子間の距離はすべて3.72Åであり,各Na原子は周囲8個のNa原子と均等な関係にある。
これを説明するために,Na-Na間の共有結合が極めて速やかに相手を変えて,いわゆる共鳴を起こしていると考えることも可能である。
(このとき電子が一部移動して,Na+とNa−とを生じ,イオン的な力も共鳴に寄与することも考えられる。)
この状態は,希ガス型電子配置を持つアルカリ金属イオンが結晶の骨組みをつくり,電子がその間を走り回って共有結合を作ったり解消したりしていると見なすことができよう。
こうして生まれた電子を自由電子ということにする。
(2)金属の帯構造理論
分子軌道法に類似した理論を用いて以上の考え方をもう少し精密化してみよう。
個々の原子の電子軌道を1s,2s,2p……のように示すと,各軌道が方位量子数に応じて一定数の電子を収容できることは前述した。
固体になった場合各軌道は幅を持った帯(たい)となり,固体を形成している原子数に応じて多数の電子を収容できるようになる。
帯の中では電子エネルギーは連続的に変化し得るものとしてよい。
帯(エネルギー帯という)の広がりは原子間距離に依存するが,最外殻nsとnpの準位が帯を形成して行く状態を図7-4に示した。
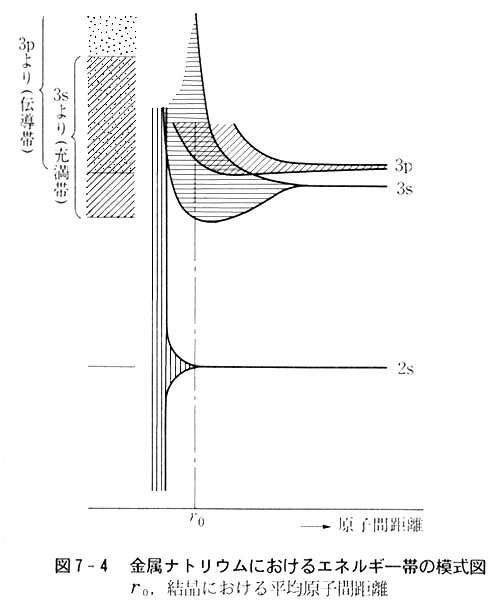
固体中では左図のようにs軌道,p軌道から生まれた帯をそれぞれ充満帯(原子価帯ともいう),伝導型と呼ぶが,両者は幅広く重なるようになる。
電子はその帯のごく一部に入っているだけになる。
このような状態になった電子が自由電子で,電場をかけると自由に電極に向かって移動できる。
電気抵抗とは,自由電子が動き回るとき,正電荷を持ったNa+イオンの格子に移動を妨げられるためで,温度上昇に伴い結晶格子の熱振動が盛んになって,妨害が著しくなる。
ここに生まれた幅広い帯を池になぞらえると,電子の状態は底のほうに水が溜った姿にたとえられる。
この帯から電子を外に出すには,水面と池の上端との差に相当するエネルギーを与える必要があるが,これが仕事関数である。
アルカリ金属ではこれが1.5〜2.5eV,1mol当りでは100〜200kJとなる。
他の単体金属では2.5〜5eVであるが,遷移元素は典型元素よりやや高い値を持つ。
