第8章 イオン結晶
イオンの作る結晶をイオン結晶という。
これらは透明で,固体ではほとんど電流を導かず,融解して液体となった時,および水に溶けた時は電導性を示す。
導電率は温度とともに上昇する。
イオン結晶の構造は少数のタイプに分類できるが,それらは大きいイオンの作る最密構造の隙間の一部または全部に相手イオンが入った構造である。
単原子イオンはもとより,多くの多原子イオンも一定の半径を持つ球に近似できる。
イオン結晶中では結合力として静電力だけが働くとして結合エネルギーを計算してよいが,多価イオンからなる場合は共有結合の寄与も考慮する必要がある。
実在のイオン結晶は決して完全なものでなく,多くの格子欠陥をもち,そのことが結晶の種々の性質を規定する。
遷移元素の化合物には不定比化合物が多いが,このことも格子欠陥と関係がある。
1.イオン結晶の構造
(1)結晶中でのイオンの配列
塩化ナトリウム(食塩)は代表的な電解質で,水に溶けるとナトリウムの陽イオンと塩化物の陰イオンに電離することはよく知られている。
結晶状態では無色透明な立方体(正六面体)となることが多いが,作り方によっては正八面体など他の形をとることもある。
天然には岩塩として巨大な鉱床を形成して産出する。
結晶中における原子(イオン)の配置を正確に決定するためには,単結晶をX線回折計にかけ,回折像を精密に解析する必要がある。(第7回)
しかし結晶系や単位格子の大きさを知るためだけなら,X線粉末回折計によって簡単に結果が得られる。
図8-1には岩塩のX線粉末回折パタンを示した。
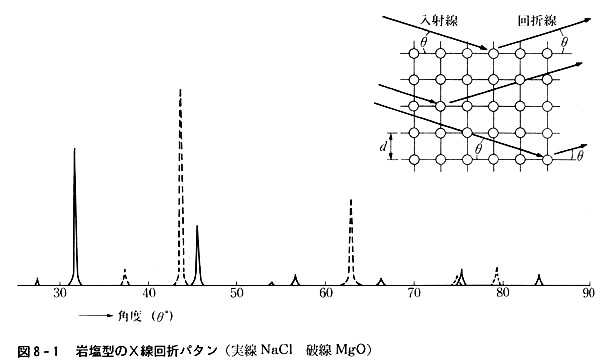
横軸は回折方向を示す角度,縦軸は回折されたX線の強度である。
海水から作った食塩の粉末も岩塩と同じ図形(パタン)を与え,外見は異なっても同一結晶を形成していることを示す。
この結晶は岩塩型と呼ばれ,立方晶系に属する。
図のような図形が現れるのは,式(8.1)(ブラッグの式)に従い,照射されたⅩ線が一定の方向に散乱されるためである。
λはX線の波長,dは原子(イオン)の間隔,θは回折角と呼ばれ,散乱X線の方向を示す。
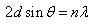 (8.1)
(8.1)
結晶中の種々なdに応じていくつかのθ方向にX線が散乱される。(nは整数で1,2…の値を持つ。)
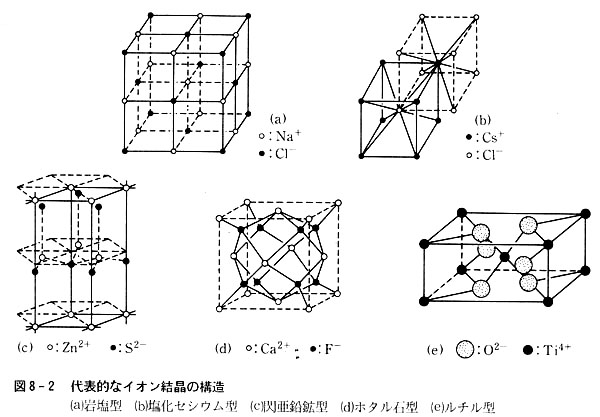
岩塩結晶中では立方体の頂点一つおきにNa+とCl-が位置しており,両イオンは最近接距離に6個の相手イオンをもつ。
(図8-2(a),配位数6を持つと表現する。)
酸化マグネシウムは,金属マグネシウムを空気中で燃焼させた時やマグネシウム化合物を空気中で加熱した時生じる白色粉末で大きい結晶にはなりにくい。
しかしX線粉末回折計にかけると図8-1の破線の結果を与える。
これは回折角が異なるだけでパタンとしては岩塩の場合と同じである。
この結晶中では,原子配列の規則性は岩塩中と同じで,図8-2(a)のNa+の位置をMg2+が,Cl-の位置をO2-が占め,Mg-O距離は2.15Åである。
また銀塩水溶液に塩化物イオンを含む水溶液を加えた時生じる塩化銀の白色沈澱も同様なパタンを与える。
これに対し閃亜鉛鉱という硫化亜鉛の鉱物は,Zn2+とS2-が1:1に結合しているが,両イオンとも配位数4で閃亜鉛鉱型または塩化銅(Ⅰ)型と呼ぶ特有の配列を持ち,それに対応するパタンを与える。
同じ硫化亜鉛でもウルツ鉱(繊維亜鉛鉱)という別の鉱物は,独自の原子配置をもつ。
またイオンの原子比1:2(2:1)の場合はホタル石型(フッ化カルシウムCaF2),ルチル型(酸化チタン(Ⅳ)TiO2),塩化カドミウム型(CdCl2)などの結晶型がある。
原子配列が複雑になると,粉末回折パタンから直接原子間距離を算出することは困難となるが,単位格子の大きさは簡単に算出できる。
このような研究を積み重ねると,イオンから生じる結晶は比較的少数の夕イプに整理できる(表8-1)。
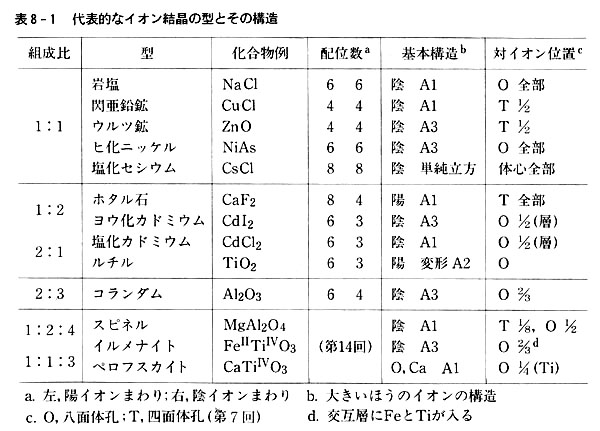
各タイプは代表的な鉱物または化合物名で呼ばれる。
(2)構造型と最密構造
イオン結晶を与える元素の種類や組み合わせは極めて多様であるのに表8-1のように少数タイプで整理が可能な理由は何であろうか。
イオンを結び合わせる静電力はどの方向にも一様に働く。
そのためまず電荷の中和されることは絶対の条件である。
一般的に陰イオンは陽イオンに比べ大きいが,陰イオンが最密構造をとり,その隙間の一部または全部に陽イオンが規則正しく入ったとするとこれらの構造を説明できる。
(ホタル石型のように陽イオンの最密構造の隙間に陰イオンが入る場合もある。)
表には陰イオンの最密構造の種類と陽イオンの入る隙間の種類を示した。
(四面体孔および八面体孔についてはp.101参照。)
(3)イオン半径
単原子イオンのように球形に近似できる場合,その大きさを示すために半径を用いるのが便利である。
しかし真空中に置いた場合,イオン周りの電子密度は電子核から離れるにつれて段々に低くなってゆくから,半径を一義的にきめることはできない。
結晶中で隣接するイオン間の距離を正確に求めることは可能であるが(式8.1),各イオンの半径を直接求めることはできず,一定の方法で実測の距離を各イオンに割り付ける。
割り付け方法は種々あるが,通常用いられるのは酸化物イオンO2-の半径を1.40Åとする方法である。
O2-は多くの陽イオンと結合してイオン結晶を与えるので基準に便利である。
表8-2のデータはこうして求めた値である。
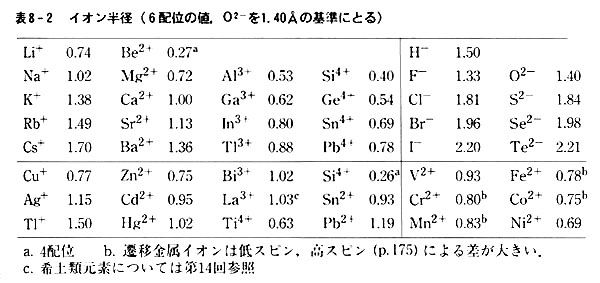
この表からは,色々の元素が与える陰陽イオンについて以下のような規則性が認められる。
1) 一元素のイオン半径はイオン価により大差がある。
陰イオンは陽イオンより大きく,陽イオンは電荷数の高いほど,陰イオンは電荷数の低いほど半径は小さい。
2)陰陽イオンとも電荷数が等しい場合,周期表の同一亜族では原子番号の大きい原子ほど半径が大きい。
3)典型元素の陽イオンでは,周期表の左から右に進むにつれて安定なイオンの電荷数が増すが,それに伴って半径は減少する。
4)遷移元素では電荷数の差による半径の差は比較的小さく,また元素間の差も小さい。
5)同一元素の同一イオンにおいては,配位数が増すほど半径はやや増加する。
(4)半径比則
イオン結晶における原子配置を考える際に重要なのは配位数である。
もし陰陽イオンとも全く変形しない剛体の球だとした場合,最密構造を持つ陰イオン球の位置を全く動かさないで,隙間に入ることのできる陽イオンと陰イオンの半径比は,簡単な幾何学の計算から,表8-3のように求められる。
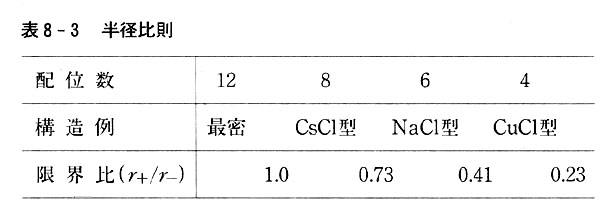
つまり陰イオンにくらべ陽イオンの半径が小さいほど陽イオンの配位数は小となる。
実際は陰イオンの位置がずれることもあるし,イオンがいくらか変形することもあるので,表のとおりにはならない。
(この点を詳しく論ずるためには許容因子という数値を用いる。この値は結晶構造タイプごとに異なるがここでは略する。)

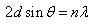 (8.1)
(8.1)


