2.格子エネルギー
(1)イオン結晶の結合エネルギー
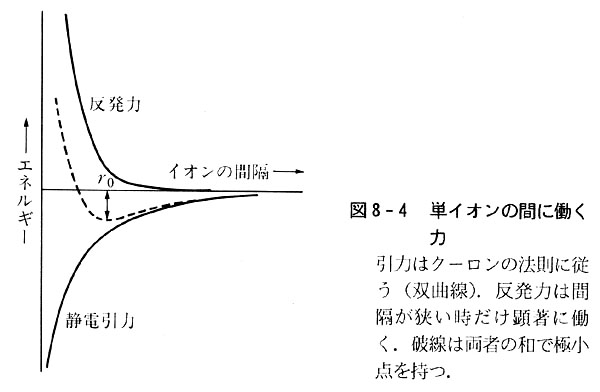
イオン結晶において原子を結ぶ力は静電引力である。
イオンどうしがあまり近づき過ぎた場合は反発力が働くが,この力は原子間距離がごく短い時にだけ顕著に働く。
この両方の力の和が陰陽イオンからイオン結晶を作るときのエネルギーで,格子エネルギーと呼ぶ(単位は通常kJmol-1)。
例 Na+(1mol)+Cl−(1mol)→NaCl(1mol)
Ca2+(1mol)+F−(2mol)→CaCl2(1mol)
(2)格子エネルギーの実験的算出
単原子イオンからなるイオン結晶の格子エネルギーは図8-3のようなサイクル(ボルン-ハーバーサイクル)を考え,ヘスの法則に基づき決定できる。
金属の気化熱,非金属単体の解離熱,金属原子のイオン化エネルギー,非金属原子の電子親和力及び化合物を25℃,1気圧の各単体から作る生成熱の各実験値が利用される。
図8-3と図2-5を比較すると,各元素単体から基底状態の原子に変えるに要するエネルギーは金属の気化熱および分子の解離熱の和である。
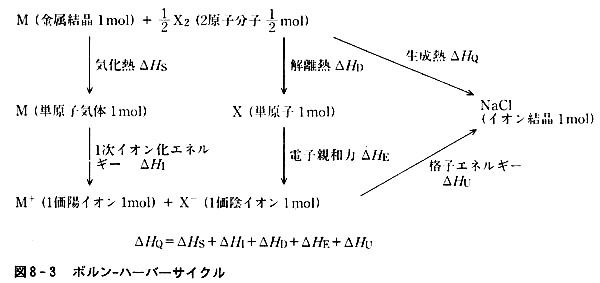
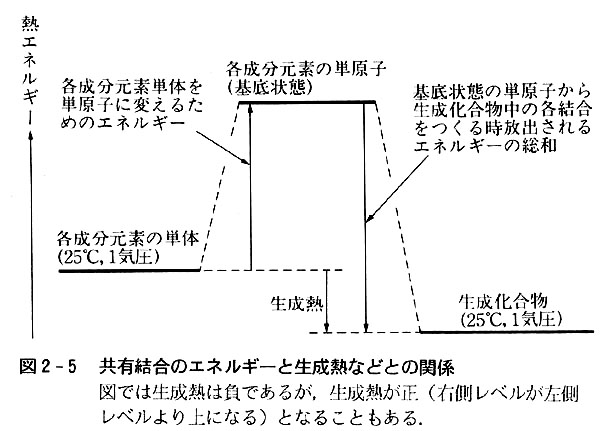
基底状態にある各元素単位を原子価状態(イオン)に変える時の励起エネルギーはイオン化エネルギーと電子親和力に対応する。
共有結合性化合物の場合は励起エネルギーの値を求めることが困難で詳しい解析は不可能であったが,イオン結晶の場合は実験的に求めやすい。
原子価状態における共有結合生成に伴って放出されるエネルギーは実験的に求めにくいが,イオン結晶の格子エネルギーと対応する。
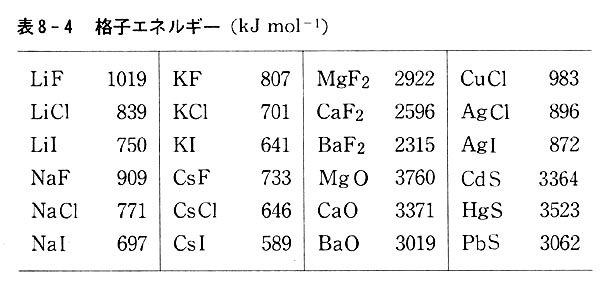
ボルン-ハーバーサイクルで求めた格子エネルギーを表8-4に示した。
(3)格子エネルギーの静電的近似
イオン結晶中に働く原子間引力は静電力で近似でき,簡単な計算で格子エネルギーのよい近似値が得られる。
a.気相におけるイオン性分子の結合エネルギー
岩塩結晶を加熱すると塩化ナトリウムの蒸気が得られるが,これはNa+とCl−からなる分子である。
(岩塩の気化熱はNa+とCl−の結合の一部を切断するのに要するエネルギーを含み,分子結晶の気化熱とは意味が異なる。)
NaCl分子の結合エネルギーは式(8.2)で近似される。
E=(e2NA/4πε0r)(1−1/n) (8.2)
eは電子の電荷,NAはアボガドロ定数,rはイオン間距離,ε0は真空の誘電率8.854×10-2J-1C2m-1である。
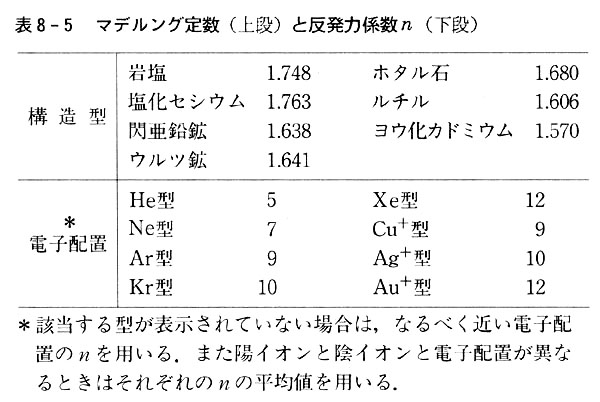
nは反発力に関する係数で,イオンの電子配置に応じて経験的に表8-5のように与えられる。
(nはまた別に指数関数で近似することもできる。)
SI単位系により,eをクーロン,rをメートル単位で示せば,Eはジュール単位で得られる。
塩化ナトリウムにおいては実測のr=2.50Å(1000℃)を用いると,結合エネルギーは485kJmol-1となる。(図8-4)
b.格子エネルギーの近似
上の考え方を格子エネルギーに適用するにはいくらかの補正が必要である。
図8-2にみるとおり,一つのNa+は多くの陰陽イオンと相互作用を持っている。r0の距離では6個のCl−と引力を,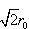 の距離では12個のNa+と反発力を
の距離では12個のNa+と反発力を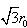 ,
の距離では8個のCl−と引力を及ぼし,さらに遠くの相手とも相互作用を持つ。
,
の距離では8個のCl−と引力を及ぼし,さらに遠くの相手とも相互作用を持つ。
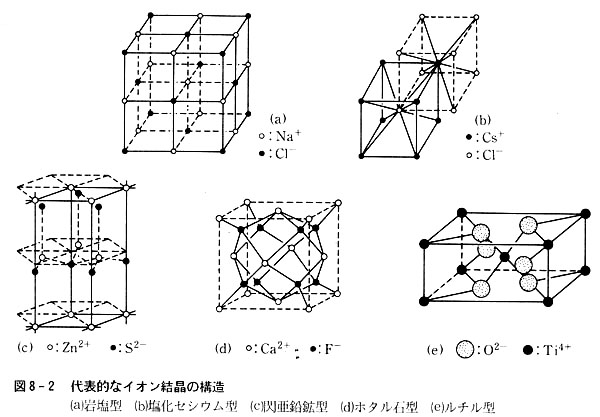
これらの相互作用の総計を示す数値はマデルング定数と呼び,幾何学的に決定されるが,結晶型に特有な数値である。(表8-5)
この補正を加え,正負イオンのイオン価Z+,Z−を考慮した一般式は式(8.3)のようになる。
E=(NAZ+Z−e2A/4πε0r0)(1−1/n) (8.3)
この式は引力としては静電力だけを考慮している。
イオン結晶に固有な値としてZ+,Z−,Aおよびr0を代入した計算値が,表8-4の実測値と一致すれば,イオン結晶中の引力として静電気だけを考えればよいことになる。
アルカリ金属イオンとハロゲン化物イオンからなる結晶をはじめ,かなり多くの低電価イオンからなる結晶においてよい一致がみられる。
(4)イオン結晶の分極
多価イオンからなる結晶や,遷移元素イオンを含む結晶においては,式(8.3)に基づく計算値は表8-4の値にくらべ小さい。
またこれらの。結晶中では,イオン間距離が陰陽イオンの半径一般値の和より短い。
つまりこれらの結晶中では静電気力以外の力が働いていると考えなくてはならない。
純粋なイオン結晶中では,陰陽イオンの原子核はそれぞれの原子の持つ電子とだけ力を及ぼしあい,陽イオンの核と陰イオンの電子との間には相互作用はないとしてよい。
もし陽イオンの原子核が陰イオンの電子を引き寄せれば,陰イオンの電子は両方の原子にいくらか「共有」されたことになる。
このような現象をイオン結晶の分極と呼ぶ。
分極の程度は陽イオンが陰イオンの電子雲を引き付ける力(分極力)と陰イオンの電子雲の変形しやすさ(分極率)に依存する。
陽イオンの分極力は,電荷数が大きいほど,電荷数が同じならイオン半径の小さいほど大となる。
陰イオンの電荷数の絶対値が大きいほど,同一電荷数ならイオン半径の大きいほど,分極率は大となる。
希ガス型電子配置をもつイオンについて,分極力および分極率の大小関係を定性的に示したのが図8-5である。

ハロゲン化アルカリにおいてはどちらも小さいため分極は生じにくく,両イオン間の力は静電力だけだと近似できる。
これに対し多価陽イオンの硫化物,窒化物などでは分極が著しい。
分極は陽イオン周りのどの方向にも一様に生じるとは限らず,結晶構造に応じある方向に著しく起こることもある。
例えばヨウ化カドミウム型では2価陽イオンはI−イオンの作る八面体孔に1段おきに入っており,分極はかなり顕著であるが,陽イオンの入った層に限られており,層状にはがれやすい性質を持つ。
多くのケイ酸塩においても,層状・線状にはがれやすいものがあるのは方向による結合力の差に基づく。(p.96)
(5)多原子イオンの場合
イオン結晶には炭酸イオン,硝酸イオン,硫酸イオンなど多原子陰イオンを含む安定な化合物が多く,工業的にも重要である。
これら陰イオンはイオンとして安定なのであって,無電荷のCO3,NO3,SO4などは安定に存在せず,これらの塩にボルン-ハーバーサイクルはそのままの形では適用できない。
またイオンの形も剛体球に近似できないものが多い。その大きさの大略の値を知るためにはいくつかの便法がある。
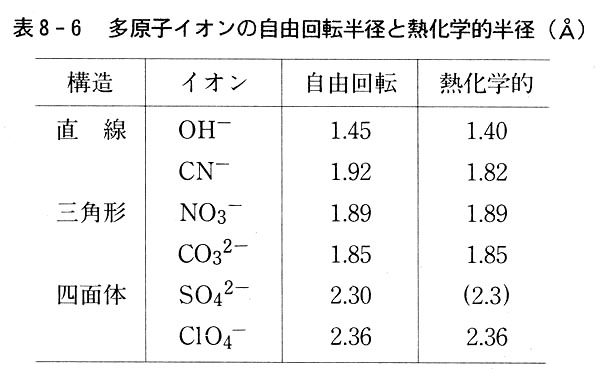
一つは結晶中でイオンは自由回転しているとみなし,形式的に球に近似したイオン半径を考える方法である。(表8-6)
一方そのような近似ができない場合でも一定の仮定のもとにイオン半径が求められることもある。
これには,マデルング定数が結晶中の平均配位数νに比例し,イオン間距離(r++r−=r0)に反比例するという経験則に基づき,式(8.3)を簡略化してマデルング定数にν/r0を代入したカプチンスキーの式(8.4)を用いる。
U=1.202νZ+Z−[1−{ρ/(r++r−)}]/(r++r−) (8.4)
1.202はNA,e2等を含む定数,ρは結晶の圧縮率から求めた反発力の定数で,イオン半径をÅ単位で表せば,UはkJmol-1で得られる。
同一構造を持ち,r+既知の2種類以上のイオン結晶について生成熱が判明すれば,式(8.2)と(8.4)を組み合わせてr−が算出される。
こうして求めた陰イオンの半径を熱化学的半径と呼ぶ。
この値は格子エネルギーを算出するためのパラメーターと考えるべき値で,陰イオンを球に近似した時の半径とは必ずしも一致しない(表8-6)。





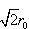 の距離では12個のNa+と反発力を
の距離では12個のNa+と反発力を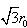 ,
の距離では8個のCl−と引力を及ぼし,さらに遠くの相手とも相互作用を持つ。
,
の距離では8個のCl−と引力を及ぼし,さらに遠くの相手とも相互作用を持つ。

