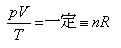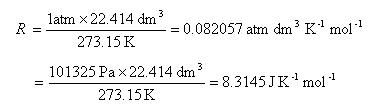3.理想気体の状態方程式
アボガドロの仮説が本当に正しいかどうかを調べる実験を紹介しよう.
先ず第一に,一定温度の下で気体の体積Vは圧力pに反比例するというボイル(R. Boyle)の法則がある.
すなわち,
 (1.1)
(1.1)
である.
図1-1に0℃において測定したいろいろな分子気体のpVの値をプロットした.
すると,気体の体積の圧力による変化には一定の傾向があることがわかる.
すなわち,(1.1)式のように気体の体積は完全に圧力に反比例しない.
その程度は,気体の種類によって異なっている.
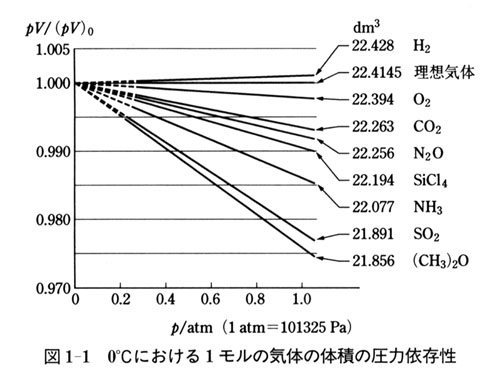
図1-1のデータによれば,(1.1)式からのずれは複雑な分子の気体ほど大きい.
しかし,どの気体も圧力無限小の極限で,
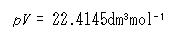
となっている.
一方,気体の体積は温度に比例するというシャルル(J.A. Charles)の法則*)がある.
これを式で表すと
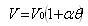 (1.2)
(1.2)
である.
ここで,θは℃単位で表した温度,V0はθ=0℃における体積である.図1-2に窒素気体の体積の温度変化をプロットした.
*)シャルルは最初に(1786-87年)気体の体積の温度変化の実験を行ったが,法則の形に整理し,実験検証を行ったのはゲー・リュサック(J.L. Gay-Lussac)であって,1802年のことであった.

この図を見ると,圧力に関わらずシャルルの法則が成立しているように見える.
しかし,より詳しく調べると圧力によってαの値が違っていることが観測される.
その結果をプロットしたのが図1-3である.
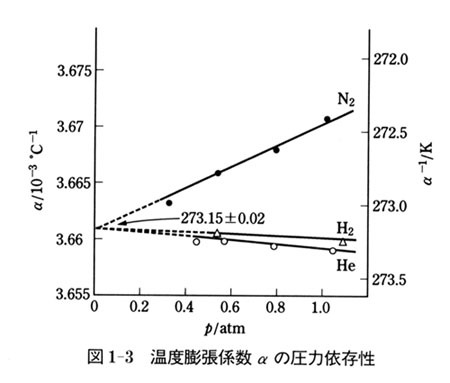
ここには,3種類の気体のαが圧力の関数でプロットしてあるが,圧力零の極限で気体の種類によらない一定値へ収斂することがわかる.
すなわち,
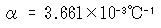
である.いま,(1.2)式を変形すると
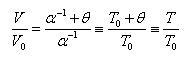 (1.3)
(1.3)
となる.
ここで,図1-3のデータより
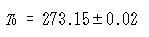 (1.4)
(1.4)
であって,絶対温度を定義することができる.
すなわち,T→0の極限では気体の体積は零となる.
ただし,この関係が成立するのは,圧力零の条件下である.
すなわち,ボイルの法則もシャルルの法則も圧力零の条件で厳密に成立する.
ここで,ボイルの法則のpV = 一定とシャルルの法則のV/T =一定を一つの式で表現すると
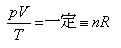
である。
ただし,気体はnモル,Rは気体定数であり,
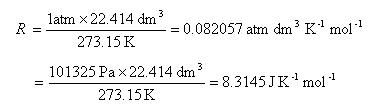
となる.
アボガドロの仮説,すなわち気体の理想状態は,p → O,V → ∞の極限の条件で成立する.この条件を言い換えると,
(1)分子は無限に小さい.つまり,分子は質点である.
(2)分子間に力が働かない.分子の運動は互いに独立である.
の2点である.
理想気体では,気体分子の区別は,分子量または分子の質量のみでなされる.
理想気体の状態方程式は,化学者が分子を直接に観察した最初の実験結果といえよう.
 (1.1)
(1.1)
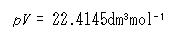
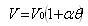 (1.2)
(1.2)

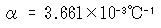
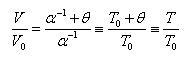 (1.3)
(1.3)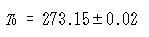 (1.4)
(1.4)