10 高分子の物性
高分子の特徴的な物性として,ゴム弾性,ゲルの物性,粘弾性,ポリマーアロイの相図・相分離を取り上げた.
ビデオ教材を活用し,数式的な展開よりも直感的に本質を理解できるように努めた.
いずれの物性も,熱力学・統計力学的な考え方をもとにし,長い分子鎖としての高分子とその分子運動性,高分子鎖の形態の多様性によるエントロピーなどを考慮に入れて展開できることを示した.
前回は,高分子の構造について述べた.
そこでは,モノマーの構造から始まって,高分子鎖の一次構造,二次構造,さらに高分子鎖集合体の高次構造が大切であることを示した.
ここでは,高分子の物性について紹介する.
高分子の物性と一口に言っても,実は複雑多岐にわたる.
代表例をまとめると,表10-1のようになる.

今回は,これらのうち特に高分子の特徴があらわれる例として,ゴム弾性,ゲルの物性,粘弾性,ポリマーアロイの相図,相分離などを取り上げる.
これらの物性の基本として,熱力学,統計力学的考え方はとても重要である.
1.ゴム弾性
ゴム弾性の特徴は,可逆的な大変形が可能なことと,超低弾性率にある.具体例を図10-1に示す.
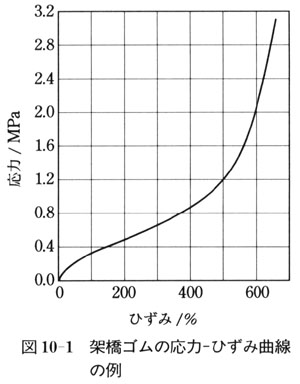
弾性率は,鉄やガラスの10万分の1のオーダーである.
またビデオ教材で示すように,ゴム糸に重りを吊るして伸張した状態に熱湯をかけると収縮する.
通常の物質は,加熱すると軟化するので,さらに伸びるはずである.
これは,ゴム弾性の本質にかかわる性質で,詳しく実験すると図10-2のような結果となる.
一定伸張下で温度を上昇させると,応力も増加する.
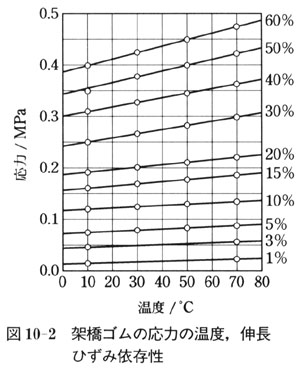
図10-2の直線を絶対零度まで外挿すると,応力は殆ど0になってしまう.これを,熱力学的に解析すると,以下のようになる.
まず,長さxで単位断面積のゴム板を,力fでdxだけ引っ張ったとする.ゴムの温度をT,圧力をp,エントロピーをS,体積をVとすると,内部エネルギーUの変化は,
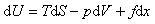 (10.1)
(10.1)
と書ける.
ここで,へルムホルツエネルギー
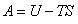 (10.2)
(10.2)
を定義する.
それは,温度,体積の関数で物質の状態変化を評価するのに都合のよい状態量である.
なお,温度,圧力の関数の対応する状態量はギブズエネルギーである.(10.1)式を用いると
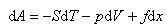 (10.3)
(10.3)
となる.
したがって,
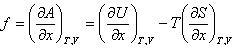 (10.4)
(10.4)
となる.
右辺の第一項は系の内部エネルギーによる力なのでこれをエネルギー弾性,第二項は系のエントロピーによる力なので,エントロピー弾性と呼ぶ.
エントロピー弾性項は,
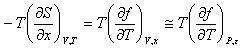 (10.5)
(10.5)
と書き換えられ実測可能な張力の温度依存性で表される.
ここで,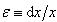 .
.
図10-2で,fを0 Kに外挿すると殆ど0になったのは,ゴムの場合,(10.4)式のエネルギー弾性が殆ど0で,大部分がエントロピー弾性によることを示している.
ゴムのエントロピーは何に由来するかというと,ゴム分子鎖の形態によるエントロピーで,分子鎖が熱運動でいろいろな形態をとることによる.
従って,ゴムは一見固体に見えるが,内部の分子鎖は液体のように激しく運動している.
その様子は,ビデオ教材に示すように,パルス法NMRを用いた水,ポリスチレン(ガラス状),ゴムのスピン−スピン緩和時間が関係した自由誘導減衰(FID)の測定比較からも明らかである.
さらに,最近ではゴム分子鎖の運動状態を分子動力学(MD)でシミュレーションすることも可能になって来たが,そのビデオ教材からも具体的なイメージがつかめるであろう.
本当のゴムでは,もっと長い多数の分子鎖が,互いに架橋されて分子運動していることになる.
ゴムは,歴史的には古代から知られた物質であるが,現在でも次々と面白い応用が拡がっている.
その例として,建物等を地震から守る免震ゴムを紹介する.
これは,ゴムと鉄板を交互に積層,接着したもので,水平方向には変形しやすいが,垂直方向には変形しにくい構造になっている.
実物の大きさは,直径40cm〜1m,高さ20〜40cm,耐荷重が50〜600t位になり,建造物の土台として使える.
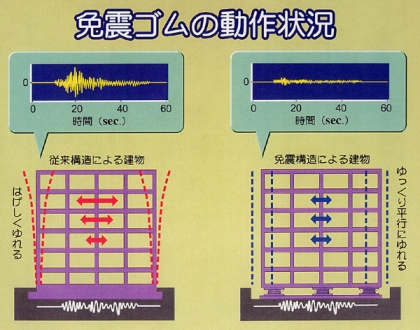
図10-3は,1995年の阪神大震災での地表,免震ゴムを使った3階建てのビルの屋上,同一敷地内の通常ビルの屋上の加速度の時間変化データである.
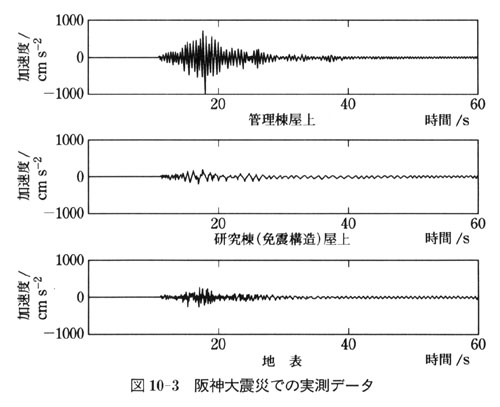
地震の揺れは約15秒で,このデー夕は震源からやや離れた場所のものであるが,地表での最大加速度は273cm s-2である.
免震棟ではそれが196cm s-2に減衰しているのに対し,非免震棟ではそれが985cm s-2にも増幅している.
こうして,建物に対する免震効果が実証されたが,更に拡げて人工地盤に応用する試み,一般家屋に応用する試みも行われている.
このような展開は,地震大国である日本でさらに進めてもらいたいものである.
同様な対策は,地震による高架高速道路の落下を防ぐための橋りょう支持部にも実施されつつある.



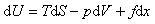 (10.1)
(10.1)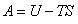 (10.2)
(10.2)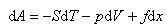 (10.3)
(10.3)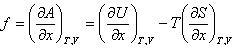 (10.4)
(10.4)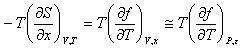 (10.5)
(10.5)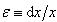 .
.
