3.粘弾性
高分子に顕著に現れる物性の例として粘弾性がある.
ビデオ教材に示すように,一見チューインガムのようにゆっくり引っ張ると粘性体のように長く伸びて元に戻らないが,まとめて机の上に落下させると弾性体のようによく弾む「はねるパテ」,一見ゴムボールで弾性体のように見えるが,机の上に落下させると粘性体のように殆ど弾まないボールなどがある.
これらは,同一物質なのに,粘性と弾性の両方の性質を持っている.
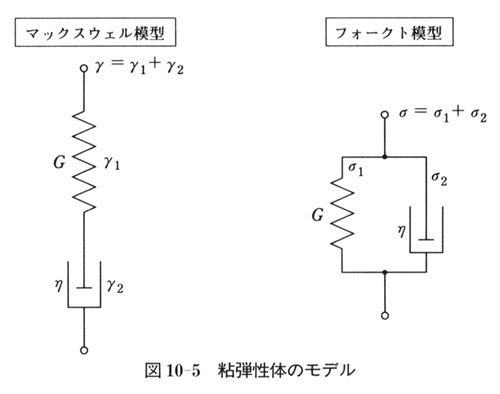
粘性をダッシュポット(粘性率η),弾性をバネ(バネ定数G)で表現すると,粘弾性体のモデルは,図lO-5のように書ける.
各要素を直列にしたものをマックスウェル模型,並列にしたものをフォークト模型と呼ぶ.
図で,γはマックスウェル模型での全体のひずみ,γ1,γ2はバネ,ダッシュポットのひずみである.
フォークト模型でσは全体の応力,σ1,σ2はバネ,ダッシュポットの応力である.
はねるパテの挙動は,定性的にはマックスウェル模型で説明できる.
すなわち,図10-5のモデルをゆっくり引っ張ると,ダッシュポットのところの変形γ2が支配的になり,ずるずると伸びる.
一方,はねるパテを丸めて机の上に落とずと,ダッシュポットの変形が間に合わず,バネが主体に効くため,よくはねることになる.
これをもう少し詳しく解析すると,マックスウェル模型にかかる応力をσとし,時間をtとすると,γ,σは(10.6)式の関係になる.
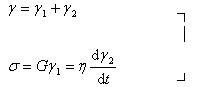 (10.6)
(10.6)
ここでは,γ1,γ2を消去すれば,
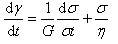 (10.7)
(10.7)
これがマックスウェル模型の基礎方程式である.
今,図10-6のように,時刻t = 0で階段状の変形γ0をマックスウェル模型に与えると,応力は,当初バネの変形によりGγ0になるが,その後,ダッシュポットの変形により減衰してゆく.
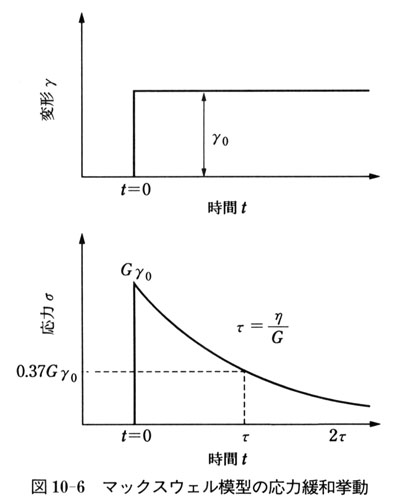
この現象を,応力緩和(stress relaxation)と呼ぶ.(10.7)式を解くと,応力の時間変化σ(t)は,
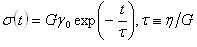 (10.8)
(10.8)
となる.
ここでτは,この系の緩和時間と呼ぶ.
従って,t =τのとき,応知よ当初の1/e = 0.37になっている.
一般に,物質の硬さを表す量として,応力とひずみの比である弾性率Gを定義するが,この場合Gは一定でなく,(10.8)式より時間依存性を持つことになる.
これを緩和弾性率G(t)と呼ぶ.
ここでは,
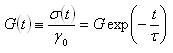 (10.9)
(10.9)
実際の高分子材料では,バネ定数の原因として,エントロピー弾性,エネルギー弾性などがあり,ηの原因としては分子鎖間のすべり,まさつなどがある.
そのためτは単一でなく,短時間から長時間まで広く分布している.
高分子の粘弾性は,従って観測時間,温度,圧力などによって大きく変化する.
図1O-7は,ポリイソブチレンのG(t)を温度,時間を幅広く変化させ,298 Kを基準にして時間依存性で表示した緩和弾性率である.
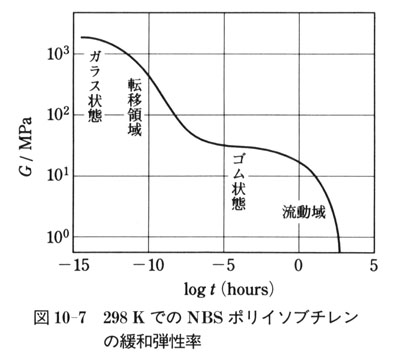
G(t)は,短時間では非常に高く,ガラス状態にあることを示しているが,時間が長くなるにつれ,転移状態,ゴム状態,流動状態と変化する.
とくにゴム状態,流動状態では高分子鎖どうしのからみ合いなどが関係している.
このような高分子の粘弾性を利用すると,衝撃,振動,音などを吸収する材料が得られる.

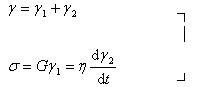 (10.6)
(10.6)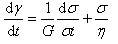 (10.7)
(10.7)
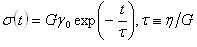 (10.8)
(10.8)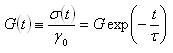 (10.9)
(10.9)