11 化学反応のしくみ(1)
われわれの身の回りにあるすべての物質は,変化の過程にある.
たとえば,われわれの環境は熱力学的に平衡状態にはなっていない.
地球をとり巻く大気の組成や構造は化学反応による生成と消滅のバランスの上に成り立っている.
この章では,化学反応がどんな速さで進行するのか,また,それを支配している因子は何かを探求する.
1.化学反応の速度
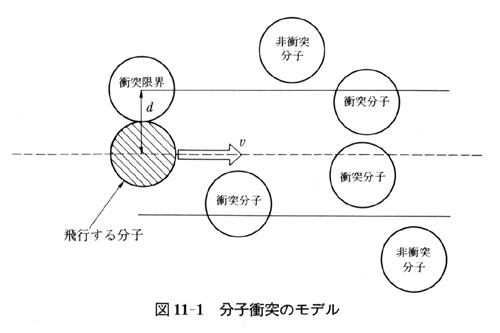
●分子の衝突
分子はそれぞれ特有な形をしているが,ここでは簡単のため球形であると仮定する.
A分子とB分子の混合気体中でA分子とB分子の衝突を考える.
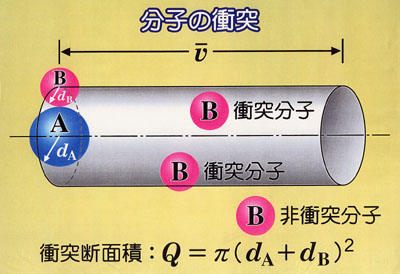
1個のA分子がB分子と単位時間に衝突する回数,衝突頻度は,A分子の半径のdAとB分子の半径dBを加えた半径d = dA + dB円の面積
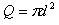 (11.1)
(11.1)
を断面積とする長さ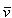 (A分子とB分子間平均速度)の円柱の中に存在するB分子の数である.
(A分子とB分子間平均速度)の円柱の中に存在するB分子の数である.

円柱の体積は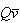 であるから,A分子1個のB分子との衝突頻度は
であるから,A分子1個のB分子との衝突頻度は
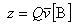 (11.2)
(11.2)
である.
ここで[B]はB分子の分子濃度である.
混合気体の中には,A分子は[A]の分子濃度で存在する.
したがって,単位体積中でのA分子とB分子の衝突頻度は
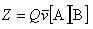 (11.3)
(11.3)
となる.
質量mの分子の平均運動エネルギーは
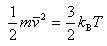 (11.4)
(11.4)
であることを1章で学んだ.
すると分子の2乗平均速度は
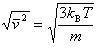 (11.5)
(11.5)
となる.
分子と速度の分布を考え,その平均をとると,(11.5)式と僅かだけ異なる値となる.
その証明はここでは取り上げないが,平均速度としては今後次の式を使うことにする.
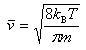 (11.6)
(11.6)
なお,A分子とB分子の間の相対速度を考えるときには,質量mには換算質量μを使わねばならない.
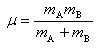 (11.7)
(11.7)
ここで,mAとmBはそれぞれA分子とB分子の質量である.
衝突頻度を1atm,25℃の窒素分子の場合について計算してみよう.
窒素分子同士の相対速度は,(11.6)式の旭を換算質量,すなわち,窒素分子の1/2の質量として計算される.
その値は670ms-1である.窒素分子のみかけの直径は0.38nmであるから,衝突断面積は4.5×10-19m2である.
また,理想気体の方程式から数密度は2.4×1025m-3,したがって,1個の分子が単位時間に衝突する頻度は
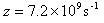 (11.8)
(11.8)
となる.
1atmの下では,分子は非常に大きな頻度で衝突している.
分子が衝突してから次の衝突まで飛行する平均距離を平均自由行程というが,それは平均速度を衝突頻度で割ったものである.
すなわち,
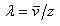 (11.9)
(11.9)
1atm,25℃の窒素分子の場合,それは9.3×10-8mである.
平均自由行程は,われわれが反応実験で用いる容器に比べて非常に小さい.
したがって,1atm程度の圧力では,分子は分子同士で衝突を繰り返し,それが容器の壁と衝突することはないと仮定してよい.
●化学反応の速度の表現
分子同士の衝突がある条件下で起これば,衝突する分子同士の化学結合の組み替えが起こる可能性がある.
つまり,化学反応が起こる.
たとえば,フッ素原子と水素の反応
F + H2 → HF + H (11.10)
では,フッ素原子が水素分子に近接して,その水素原子を「引き抜く」反応を行う.
原子やラジカル(不対電子をもつ分子)が反応分子と衝突した場合,反応が起こる確率は高い.
原子やラジカルは,安定に存在する分子の結合を切断することによって生成される.
したがって,それは他の分子を攻撃してその結合を切断して自らが安定分子になろうとしたり,それら同士が再結合したりする活発な分子である.
このように反応活性に富む化学種は,衝突毎に反応を引き起こす.ここで,衝突と反応速度との関係を考えよう.

いま,分子Aと分子Bとが反応して,生成物CとDを生成する反応を考える.
A + B → C + D
反応速度は,反応物の濃度の減少速度,生成物の濃度の増大速度で表現できる.
すなわち,
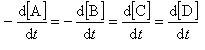 (11.12)
(11.12)
である.
この速度はAとBの衝突頻度に比例する.
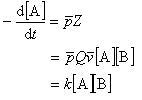 (11.13)
(11.13)
ここで,kを反応速度定数といい,AとBがそれぞれ単位濃度の時の反応速度である.
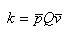 (11.14)
(11.14)
であって,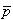 は衝突の反応確率である.
は衝突の反応確率である.
反応速度定数の次元は(11.11)式のような2体衝突の場合
[濃度]-1[時間]-1
である.
普通,濃度の単位は,mol cm-3またはmolecule cm-3とすることが多いので,kの単位はmol-1 cm3 s-1,または,molecule-1 cm3 s-1である.
化学反応の進行は,反応分子の濃度を時間の関数で描くことによってより理解し易い.
(11.13)式でt = 0の濃度を[A]0,[B]0とすると,反応の途中で
[A]0 - [A] = [B]0 - [B]
の関係がある.
したがって,(11.13)式は
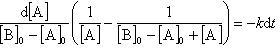 (11.15)
(11.15)
となる.
両辺を積分すれば,
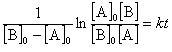 (11.16)
(11.16)
この反応で[B] >> [A],つまり,大過剰のBの中に反応分子Aを混合したとき,反応によるBの減少は無視できる.
すると,(11.16)式よりAの濃度は,
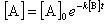 (11.17)
(11.17)
の式に従って,Aの濃度はその初期濃度[A]0から
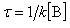 (11.18)
(11.18)
の時間で (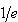 = 1/2.7)となる.
= 1/2.7)となる.
この時間をAの寿命といい,反応速度の別の表現となっている.
空気中で1個の窒素分子や酸素分子が他の分子と衝突する頻度は約3×109s-1である.
いま,反応分子Aや反応相手分子Bの大きさやその質量(分子量)が,空気中の窒素や酸素と同じであると仮定する.
すると,1気圧,25℃の下では,反応分子は同程度の衝突を持つと考えてよい.
もし,1回の衝突で反応が起こる,つまり,衝突の反応確率が1であれば,1気圧の空気中の中で反応分子の寿命は3×10-10sという短いものとなる.
そのときの速度定数は,1気圧の分子密度が2.5×1019molecule cm-3 = 4.1×10-5mol cm-3であるから,衝突頻度をこれで割った値,すなわち
k = 1×10-10 molecule-1 cm3 s-1
= 1×1015 mol-1 cm3 s-1 (11.19)
となる.
2体衝突に基づく化学反応(これを2分子反応という)の速度定数の上限は,(11.19)式で与えられる.
衝突の反応確率の大きさは,反応によってさまざまである.
空気の組成が窒素と酸素でほぼ全体を占めていることは,それらの分子同士の衝突の反応確率が極めて小さいことを意味する.
酸素はいろいろな物質を酸化する働きをするが,窒素との反応で,
N2 + O2 → 2NO (11.20)
のように窒素酸化物を作る反応速度は極めて小さい.
そうでなければ,大気中の酸化窒素の濃度はもっと大きいはずであるし,空気の組成も今とは違ったものとなっているであろう.
●頻度因子と活性化エネルギー
擬一次反応の手段で
O + RH → OH + R (11.21)
の反応,酸素原子がアルカンRHから水素原子を引き抜く反応の速度定数をいろいろな温度で測定した例を示そう.
この反応速度の測定のためには,SO2/RH/Arの混合気体を衝撃波で加熱し,いろいろな温度とし,その気体に波長193nmのレーザー光パルスを照射してSO2 → SO + Oの光解離反応によって瞬間的にO原子を生成させる.
O原子は(11.21)の反応によって擬一次反応で減少する.
その速度をアルカンの濃度で割り算すれば,(11.21)の反応の速度定数を求めることができる.
そのデータを示したのが図11-2である.
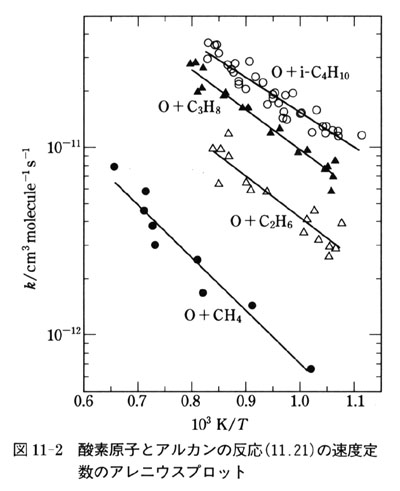
この図では,速度定数の対数が1/Tの関数でプロットしてある.
その結果,反応速度定数の値は温度の関数で
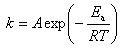 (11.22)
(11.22)
この反応速度定数の関係を最初に発見した人の名をとって(11.22)式をアレニウス(S.A.Arrhenius)の式という.
ここで,Aは頻度因子,Eaは活性化エネルギーという.
化学反応が反応分子の衝突で起こるという立場で(11.21)式を解釈すると,(11.14)式と比較すればよい.
すると,
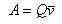 (11.23)
(11.23)
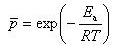 (11.24)
(11.24)
となる.
頻度因子は反応分子同士が衝突する頻度である.
反応の衝突確率は,衝突の中でも反応分子同士の相対運動のエネルギーが活性化エネルギーEa以上である確率を表現する.
反応が起こるためには,ただ,衝突するだけではなく,一定以上のエネルギーが要求される.
このエネルギーは,反応分子の衝突対が,生成分子へ変化する途中の最高のエネルギー状態に相当する.
このような状態は,活性化状態または遷移状態と呼ばれる.
それは,反応分子から生成分子へ至るポテンシャルエネルギーの最高値に当り,いわば反応の道すじの峠の頂上の高さに相当している.
反応速度定数の温度依存性の測定からその値を求めることができる.
現在までに,多くの反応速度定数の測定がなされ,データベースとなっている.
表11-1にはいくつかの例を与える.

反応[1]〜[5]の速度定数の頻度因子が10-10〜10-11であるのは,衝突頻度の見積りに一致している.
ただ,反応[3]の頻度因子だけが他に比べてやや,小さくなっている.それは,衝突が
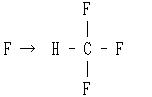
の形式で進んだときのみ反応が起こり,
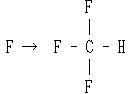
の方向の衝突では反応確率が小さいからである.
すなわち,衝突の方向性を考慮した立体因子を導入する必要がある.
フッ素原子の反応と酸素原子のそれとを比較すると,反応相手分子が同じであっても活性化エネルギーが酸素原子の反応でずっと大きくなっている.反応試剤によって活性化エネルギーは大きく変わる.
フッ素原子は極めて活性な反応試剤であって,25℃の温度の下でもほとんど衝突毎に反応が進む.
一方,酸素原子も活性に富んでいるが,25℃では106〜107回に1回反応が起こる程度である.
これが1500℃以上の高温になると酸素原子の反応は100回の衝突に1回位の高頻度で反応を行うようになる.
酸素原子の反応が燃焼のような高温度で重要な役割を演ずるのは理解できる.
表11-1の反応[6]と[7]は,単純な2体衝突では説明できないものである.
反応[6]では,酸素原子と酸素分子が会合してオゾンを生成する.
この反応は106kJmol-1の発熱反応で,エネルギー的にはオゾンの方が安定である.酸素原子と分子の衝突を2体反応で考えると,
O + O2 → O3* (11.25)
のように,生成した衝突錯合体O3*は,このままでは過剰エネルギー106kJmol-1を持っているため,短い時間内に再び解離し,もとの原子と分子に戻ってしまう.
安定なオゾンを生成するためには,エネルギー過剰なオゾンを安定化させるための第3の衝突が必要である.
すなわち,
O3* + M → O3 + M (11.26)
のように,過剰エネルギーを取り除く媒体として第3体Mとの衝突が必要である.
すなわち,表11-1の反応[6]では酸素分子が,反応[7]では,アルゴン原子がその役割を演じている.
反応[7]は,二つの酸素原子が再び結合して分子を作る反応である.
この場合にも第3体を必要とする.
このように,安定な分子を生成物とする反応では,結合の組み替えという観点からは無関係な第3体分子が,反応の進行に対して重要な役割を演ずる.その反応速度は,
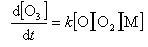 (11.27)
(11.27)
のように3分子反応となる.
この場合,反応速度定数は
[濃度]-2[時間]-1
の次元をもつ.
また,その速度定数は,(11.21)式のように頻度因子と活性化エネルギー項から成る形式をとらず,温度の上昇とともに速度定数が小さくなる.
それは,再結合反応では,活性化状態よりも第3体衝突によるエネルギー移動が反応を支配しているためである.
化学反応速度定数がどのように温度依存性を示すかをわかり易くするために,図11-3に二つの反応
H + O2 → OH + O (11.28)
H + O2 + N2 → HO2 + N2 (11.29)
の速度定数のアレニウスプロットを示した.
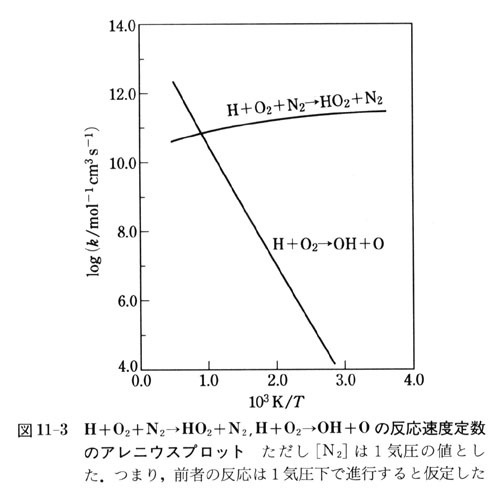
アレニウスプロットとは,速度定数の対数を温度の逆数の関数でプロットしたものである.
速度定数が(11.22)式のようにアレニウス式であれば,プロットは1/Tに対して負の勾配をもつ直線となる.
反応(11.28)の速度定数の温度依存性はアレニウス式とよく一致し,A = 1.4×1014mol-1cm3s-1,Ea = 67.2kJmol-1である.
この反応では,Aが衝突頻度に近く,単純な衝突の考え方でほぼ理解できる.
一方,反応(11.29)は,3分子反応の付加反応で,その活性化エネルギーは零と考える方が順当である.
N2の圧力が1気圧としたときの2分子反応として速度定数(k[N2])をプロットした.
速度定数は,衝突頻度に近く,温度の上昇とともに小さくなる傾向がある.
一般に,反応速度には,強い温度依存性を示す活性化エネルギーを持つアレニウス式で表されるものと衝突頻度に近く,温度依存性のほとんどないものの二つの夕イプがある.

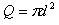 (11.1)
(11.1)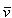 (A分子とB分子間平均速度)の円柱の中に存在するB分子の数である.
(A分子とB分子間平均速度)の円柱の中に存在するB分子の数である.
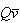 であるから,A分子1個のB分子との衝突頻度は
であるから,A分子1個のB分子との衝突頻度は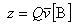 (11.2)
(11.2)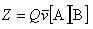 (11.3)
(11.3)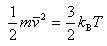 (11.4)
(11.4)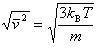 (11.5)
(11.5)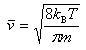 (11.6)
(11.6)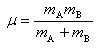 (11.7)
(11.7)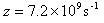 (11.8)
(11.8)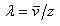 (11.9)
(11.9)

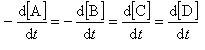 (11.12)
(11.12)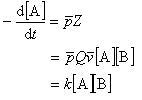 (11.13)
(11.13)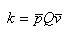 (11.14)
(11.14)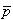 は衝突の反応確率である.
は衝突の反応確率である.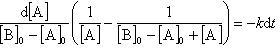 (11.15)
(11.15)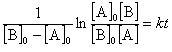 (11.16)
(11.16)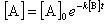 (11.17)
(11.17)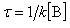 (11.18)
(11.18)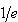 = 1/2.7)となる.
= 1/2.7)となる.
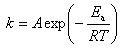 (11.22)
(11.22)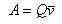 (11.23)
(11.23)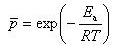 (11.24)
(11.24)
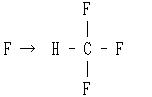

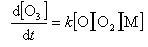 (11.27)
(11.27)