2.温度
気体の中では,分子は自由に飛び廻っており,理想気体の条件下で,その運動エネルギーは絶対温度に比例することが実験で示された.
この場合,セルシウス(A. Celsius)温度θ(1 atmにおける水の氷点をO℃,
沸点を100℃とする温度目盛)で温度を定義しておくと,
気体の体積がゼロとなる温度が定義され,その温度は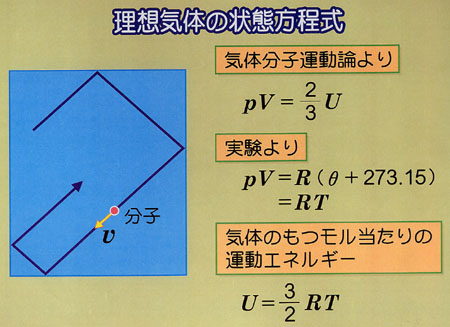
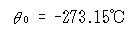
となることが実験で示された.
マイナスの体積というのは物理的に意味をなさないので,
この温度が可能な最低の温度ということになり,この温度をゼロとする絶対温度
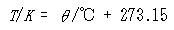 (2.1)
(2.1)
が定義される.
絶対温度は,熱力学の創始者の一人であるケルビン(Lord Kelvin, W. Thomson)の頭文字をとった記号Kを用いて表示される.
従来の温度は,二つの温度定点の間を等分して定義した「目盛」であったのに対し,絶対温度は他の物理量と同じように「単位」で表現される.
現在,単位Kは,後の章で説明する水の三重点の1/273.16と定義されている.
理想気体の状態方程式から絶対温度の概念を説明したが,それ以外に次の二つの事実を挙げることができる.
第一はカルノー機関の効率が高温熱源の絶対温度THと低温熱源の絶対温度TLのみで定まり,その効率は1-(TH /TL)で与えられるという事実である.
ケルビン卿はカルノーサイクルの重要さに着目し,熱力学第二法則を導くと同時に,熱力学的温度を提唱した.
カルノーサイクルは熱力学の基礎をなす思考実験であるが,この講義ではその詳細を付録6に説明し,教科内容には含めない.
第二は,統計力学による温度の意義である.
第4章で,温度Tの分子集団でエネルギーεをもつ量子準位に分布する確率は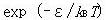 であることを説明する.
であることを説明する.
それは分布の仕方の数が最大となるような分布である.
ボルツマン分布の導出も本教科の範囲外であるので,付録5にその詳細を説明する.
ボルツマン分布の意味を解釈すると温度は分子の一つの運動自由度当りに分配する平均エネルギーを与える.
熱力学では絶対的な温度が定義されるが,ミクロに考えると分子の多数の集団の平均エネルギーに相当している.

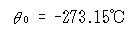
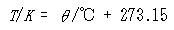 (2.1)
(2.1)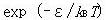 であることを説明する.
であることを説明する.