1．状態の無秩序さ
●状態変化の方向
平衡状態にある物質の温度や圧力を変えたり，他の物質を混合したりしたとき，どんな変化や反応が起こるかは，化学者にとって大変興味がある．
自然に起こる反応で一番身近にあるのは，燃焼である．
周辺にある物質の多くは，空気中の酸素と化合して酸化物になる．
その理由として誰でも考えるのは，燃焼反応が大きな発熱をともなうという事実である．
確かに，発熱反応なら自発的に反応が進行するが，吸熱反応では外から熱を加える必要がある．
しかし，吸熱反応でも相当速い反応がある．
たとえば，炭酸ナトリウム水溶液と塩化カルシウム水溶液を混合したときの炭酸カルシウム生成の沈殿反応は吸熱である．
反応が自発的に進むかどうかの判断材料として，反応にエネルギーを必要とするかしないかだけをとりあげるのには問題がある．
何故なら，反応する系とそれをとり囲む外界の全部を考えると，内部エネルギーは保存されるからである．
つまり，定温・定積の過程を考えると，系にとっての発熱は，外界にとっての吸熱である．
したがって，エネルギーのような保存量だけで，状態変化の方向の判断をすることはできない．
この章では，状態変化の方向を定める状態量は何であるかを探ることにする．
●確率の力
気体が容器のなかに入っている場合を考える．
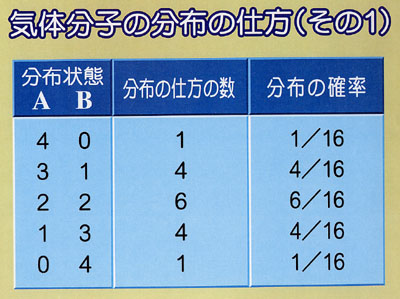
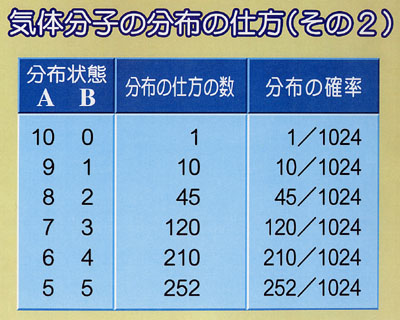
容器を左半分と右半分に区切って，そのどちらに気体分子が存在するかを考える．
まず，第1の分子が左半分に存在するか，右半分に存在するかの確率はそれぞれ1/2である．
第2の分子についても同様で，それぞれの部分に存在する確率は1/2である.
すると,
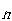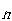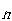個の分子のすべてが容器の片側の半分に存在する確率は1/2である．がアボガドロ定数の程度であれば，その確率は零であるといってよい．したがって，「容器の半分をすべての分子が占める」の反対の事象が起こる確率が非常に1に近いことになる．
つまり，気体分子は容器の中に均一に分布する．
分子数が少ない場合には，容器の中で分子密度が偏る確率はそんなに小さいものではない．
しかし，われわれの扱っている系が極めて多くの分子から成るために，確率による予測に確信が持てるわけである．
このような分子の分布状態の予測の方法をわれわれの関心のある物質の系に応用して，でき上がった学問大系が統計力学である．
それは気体のマクロな性質を気体分子の運動で説明しようとしたマクスウエル（J.C. Maxwell）とボルツマン（L. Boltzmann）の19世紀後半の研究に始まり,ボルツマンがエントロピー増大則を確率論的にとらえる原理を提案して，統計力学の基礎が築かれた．
●分子の量子準位分布の統計
分子には，その運動 −並進，回転，振動− に応じて，一定の量子数で指定される量子準位があって，分子はそのいずれかに所属する．
分子がどの量子準位をとるかは，前述の「確率の力」で定まる．つまり，分子は実現可能性のもっとも大きい準位への分布の仕方をとるであろう．
実現可能性のもっとも大きいのは，多数の分子をいろいろな量子準位へ分布させる仕方の数
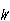が最大となる場合である．いま，量子数1，2，…の量子準位に所属する分子の数がそれぞれ
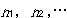であるとする．すると，
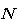個の分子をそれぞれの準位に分布させる仕方の数は，
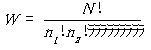(4.1)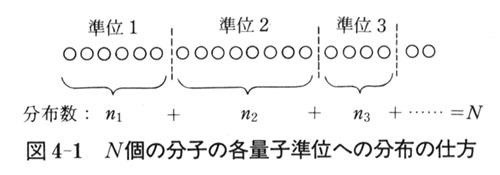
となる．
分子の各準位への分布は，図4-1のように分子を順番に並べて最初から
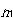個の所に仕切りを入れ，次に，
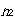個の所に仕切りを入れるという風にすることと同じことである．すると，分子の並べ方が
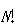通りあるのに対し，各仕切りの中では，分子は同じ準位をとるので，その並べ方の区別は意味はない．したがって，それぞれの仕切りの中での並べ方の分だけ数え過ぎているわけで，
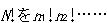で割り算したものが分布の仕方の数となる．次の問題は，
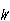が最大になるような
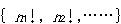の分布を探すことである．前節で容器の中で気体分子がどのように分布するかを考えた．
その場合には，分子が容器の中のどこに存在するかによってエネルギーは変わらないから，分子は容器中に均一に分布する場合の実現可能性がもっとも大きい．
つまり，各量子準位のエネルギーが等しければ,
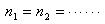
の分布が
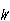を最大にする．ただし，分子の総数は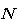であるから
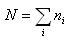(4.2)の条件は満たされなければならない．
一般には，分子の各量子準位は固有のエネルギー
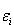を持っている．すると,
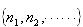の分布の場合の全エネルギー
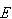は，
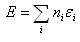(4.3)となる．
いま，
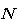個の分子の持つ全エネルギーは，エネルギー保存の原則によってどんな分布状態でも一定である．すると，もっとも実現可能性のある分布は，（4.2）と（4.3）式の条件下において
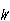を最大にする分布であり，これを探す必要がある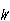．が最大値であれば，ln 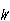も最大である．ln
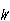を最大とする分布
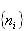の計算を最初に行ったのはボルツマンで，その分布をボルツマン分布という．その計算の詳細に興味をもたれる方は付録5を参照されたい．ここでは，結果のみを示す．
準位エネルギー
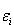をもつ1番目の量子準位に分布する最大確率の分子数は
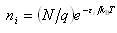(4.4)である．ここで，
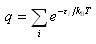(4.5)は分配関数である．
分配関数は，大変大切な物理量で，これからすべての状態量を導くことができる．
ボルツマン分布の性質を少し調べておこう．
（4.4）式の指数関数の指数をみると，高い温度では
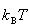が小さい．その場合，エネルギーの高い準位まで分布することになる．
一方，低い温度で
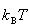が大きい場合，エネルギーの低い準位にのみ分布するようになる．このことは，分子の運動自由度に対するエネルギー分配の量子効果として説明したことである．
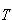→ 0の極限では，すべての分子が最低の準位に分布するようになる．つまり，分布の可能性は一通りしかない極限的状態となる．一方温度が十分高い場合には，図2-3に示したように準位間隔が に比べてずっと小さくなり，分子はエネルギー保存の条件を満足すればどの準位にも自由に分布することができる．
これがエネルギー等分配則が成立する場合である．
●ボルツマンの原理
物質の状態変化は，物質を構成する分子の準位分布の可能性の大きい状態へ向かって起こる．
すると，ある状態から別の状態へ移行するかどうかを判断するのに，状態に固有な「分布の可能性」を表すパラメーター，すなわち，状態量を定義する必要がある．
ボルツマンは，エントロピーという状態量と分子の状態分布の仕方の数
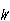とを
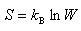(4.6)
の式で関係づけた．
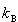はボルツマン定数で，1章の気体運動論で導入された定数である．この式は，物質の状態を原子分子の量子準位への分布の確率で判断する統計力学の基本式である．
後にエントロピーの考え方は，社会現象にまで応用できることが分かった．
その大きなインパクトの故かウィーン中央墓地にあるボルツマンの墓（図4-3）にはこの式が刻まれている．
この式によって，ボルツマンはエントロピーが「状態分布の可能性または無秩序さ」を表現するものであることを明らかにした．
確率の力によって物質の状態変化の方向が定まるとすると，それは
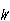の増大，つまり，エントロピーの増大の方向に向かって起こる.エネルギーは量だけでなく「秩序さ」といういわば価値を持っている．
熱というのは本質的にばらばらである．
自然のプロセスは，無秩序への崩壊を表す．次の節では，エントロピーの熱力学上の意義を考えよう．