2.熱力学におけるエントロピーの定義と意義
●可逆と不可逆
物質の状態変化が起こる場合,ある一定の量のエネルギーの移動が起こる.
それは,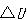 が最初と最後の状態によって決まるからである.
が最初と最後の状態によって決まるからである.
そのエネルギー移動はいくつかの形で起こる.
たとえば,系と外界に温度差があれぱエネルギーは熱の形で移動する.
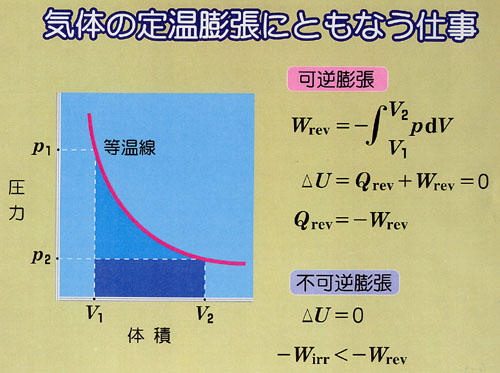
また,気体の膨張のように仕事の形をとることもある.それは,熱力学第一法則で
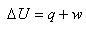 (4.7)
(4.7)
のようにまとめられている.
ここで,変化を行う可能性のうち両極端のものについて考えてみよう.
気体が体積 へ膨張する場合である.
へ膨張する場合である.
そのとき外界から加えられている外圧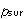 に対抗して膨張するわけで,エネルギーを仕事という形で外界に伝える.
に対抗して膨張するわけで,エネルギーを仕事という形で外界に伝える.
すなわち,
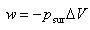 (4.8)
(4.8)
である.
ここで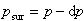 のように系と外界の圧力がいつも釣り合うように膨張させたとする.
のように系と外界の圧力がいつも釣り合うように膨張させたとする.
このとき膨張にともなってなす仕事は最大である.
この膨張過程は,外界の圧力をや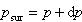 とすれば,逆に圧縮過程とすることができる.
とすれば,逆に圧縮過程とすることができる.
つまり,変化は可逆過程である.
実際には,外圧を内圧といつも等しくすることはできない.
したがって,現実に起こる膨張は不可逆で,外界に対してなす仕事は最大値より少ない.
しかし,系を元の状態に復帰させるためには,外界は系に対して少なくとも可逆仕事に等しいだけの仕事をしなければならない.
したがって,外界は,系に対して返さなければならない量より少ない仕事を受けとったことになる.
その代わり,外界は後で系に返さねばならない量より多くの熱を受けとる結果となる.
結局,系を元の状態に戻したことによる正味の結果は,外界が仕事をなし得る能力を減らしたということである.
系が可逆的に変化するときだけ系と外界の両方が最初の状態に復帰できる可能性がある.
可逆,不可逆の相違をボルツマンの提案した分子の状態分布の可能性,すなわち無秩序さの概念を使ってまとめてみよう.
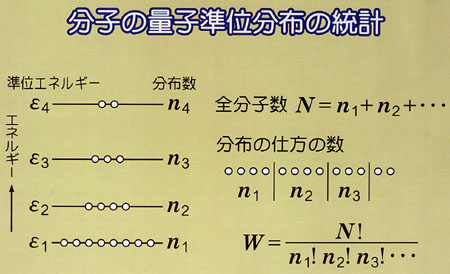
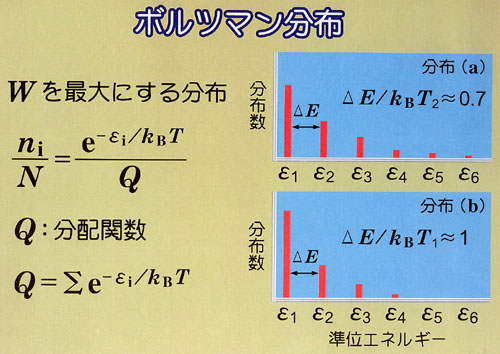
可逆過程では,系に生じた無秩序が外界に生じた秩序の増加で丁度帳消しにされる.
不可逆過程では,系で増加した無秩序は,外界で増加した秩序の増加と完全に釣り合っていない.
系をもとの状態へ不可逆的に戻そうとすると,系の秩序の増加は外界の無秩序の増加を下回ることになろう.
したがって,系は元の状態に戻って仕事をなし得る能力を回復しているが,そのために,外界はその仕事の最大値以上の仕事をしなければならない.
したがって,系と外界の正味の結果は,外界の無秩序の増加が残ることになる.
●熱力学第二法則

エントロピーは,状態変化の不可逆性の度合いを表す状態量であるとも解釈できる.
それはクラウジウス(R.J.E. Clausius)が命名した状態量でギリシャ語の「変化」に由来する.
系が一定温度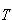 で状態変化を行うとき,系のエントロピー変化
で状態変化を行うとき,系のエントロピー変化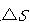 は,その変化を可逆過程で行わせたときに系へ移動する熱量
は,その変化を可逆過程で行わせたときに系へ移動する熱量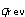 を温度
を温度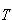 で除したものに等しい.
で除したものに等しい.
すなわち,
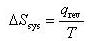 (4.9)
(4.9)
と定義される.
このクラウジウスの定義したエントロピー変化と(4.6)式のボルツマンのエントロピーとは,等価であることは証明できる.
マクロな観点の熱力学とミクロな考え方を基礎にした統計力学が同じ結論に導くことは極めて興味深いことである.
エントロピーは状態量である.変化がどう行われようと,可逆過程の熱の移動は一通りしかない.
つまり,系の最初と最後の状態によって定まる.
これに対して,外界のエントロピーの変化は系の変化の道すじで変わる.
可逆過程の場合,系のエントロピー変化,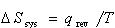 と外界のエントロピー変化,
と外界のエントロピー変化,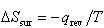 とは互いに打ち消し合い,系と外界の全体のエントロピー変化は無い.
とは互いに打ち消し合い,系と外界の全体のエントロピー変化は無い.
一方,不可逆過程での外界のエントロピー変化を熱の移動量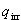 で表すと,
で表すと,
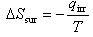 (4.10)
(4.10)
となる.*)
*)ここで,エントロビー変化が不可逆過程の熱の出入り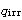 を使って定義できるという意味ではない.
を使って定義できるという意味ではない.
系と外界の全体のエントロピー変化は,
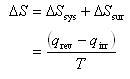 (4.11)
(4.11)
である.
前項の討論で,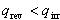 である.したがって,
である.したがって,
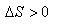 (4.12)
(4.12)
である.
ここで,われわれは,物質の状態変化について一つの公理に到達する.
それは熱力学第二法則として知られている.
残念ながら,第二法則は第一法則のように厳密な形で数式で書き表すことはできない.
それは,次のような文章で表現される.これらの文章は互いに等価な内容をもっている.
「宇宙のエネルギーは一定であるが,宇宙のエントロピーは増加する.」
「外界から熱を吸収して外界に何の影響も残さずに仕事を生み出す機械を作ることはできない.」
「熱を低温物体から高温物体へ他に何の影響も残さずに移動させることはできない.」
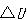 が最初と最後の状態によって決まるからである.
が最初と最後の状態によって決まるからである.
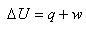 (4.7)
(4.7)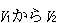 へ膨張する場合である.
へ膨張する場合である.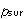 に対抗して膨張するわけで,エネルギーを仕事という形で外界に伝える.
に対抗して膨張するわけで,エネルギーを仕事という形で外界に伝える.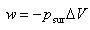 (4.8)
(4.8)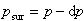 のように系と外界の圧力がいつも釣り合うように膨張させたとする.
のように系と外界の圧力がいつも釣り合うように膨張させたとする.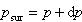 とすれば,逆に圧縮過程とすることができる.
とすれば,逆に圧縮過程とすることができる.


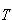 で状態変化を行うとき,系のエントロピー変化
で状態変化を行うとき,系のエントロピー変化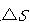 は,その変化を可逆過程で行わせたときに系へ移動する熱量
は,その変化を可逆過程で行わせたときに系へ移動する熱量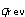 を温度
を温度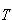 で除したものに等しい.
で除したものに等しい.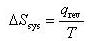 (4.9)
(4.9)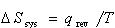 と外界のエントロピー変化,
と外界のエントロピー変化,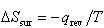 とは互いに打ち消し合い,系と外界の全体のエントロピー変化は無い.
とは互いに打ち消し合い,系と外界の全体のエントロピー変化は無い.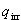 で表すと,
で表すと,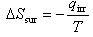 (4.10)
(4.10)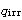 を使って定義できるという意味ではない.
を使って定義できるという意味ではない.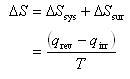 (4.11)
(4.11)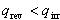 である.したがって,
である.したがって,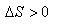 (4.12)
(4.12)