第5章 化学平衡
物質の状態を定めているのは,物質固有のエネルギー,エンタルピーとその無秩序さを表すエントロピーであることを知った.
この二つの状態量を活用して物質の化学平衡状態を探究する.
その際,エンタルピー,エントロピーを統合して平衡状態を記述する新しい状態量,ギブズエネルギーを導入する.
この章では,化学平衡定数をギブズエネルギー変化によって解明する.
1.平衡の条件
●ギブズエネルギー
 平衡状態は,物質の状態変化の自発的な不可逆過程がこれ以上起こらない状態である.
平衡状態は,物質の状態変化の自発的な不可逆過程がこれ以上起こらない状態である.
したがって,状態は時間が経過しても変化しない.
すると,自発的な過程がどのような場合に起こるかを考えることが,平衡状態を判断するための条件を与えるはずである.
自発的変化は,系のエンタルピーが減少する場合,
 (5.1)
(5.1)
また,系のエントロピーが増加する場合,
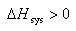 (5.2)
(5.2)
の条件下で起こりやすい.
前の章で,エンタルピー変化は系と外界の両方を考えるとゼロになるので,変化の方向の判断材料にならないと述べた.
それにもかかわらず系の発熱過程が起こり易いのは,外界への熱の移動によるエントロピーの増大の可能性があるからである.
(5.1〜2)式がともに満たされている変化もある.
しかし,片方の条件が満たされているが,他方は不都合な場合もある.
たとえば,液体が蒸発する場合, は正で不都合であるが,
は正で不都合であるが, は正で条件を満たしている.
は正で条件を満たしている.
原子の再結合反応で分子を生成する反応では,逆に, で都合が良いが,
で都合が良いが,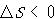 で不都合である.
で不都合である.
そこで,この二つの因子を一つにまとめた新しい状態量を導入し,一つの因子で状態変化の可能性を判断することが考えられる.
ギブズ(J.W.Gibbs)はそのような新しい状態量を提案し,それはギブズエネルギー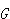 と呼ばれている.
と呼ばれている.
それは
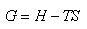 (5.3)
(5.3)
と定義されるが,温度一定,圧力一定の条件下の変化では,
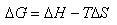 (5.4)
(5.4)
となる.
温度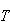 を
を に掛けたのは,単位をエネルギーの次元に統一するためである.
に掛けたのは,単位をエネルギーの次元に統一するためである.
(5.4)式のギブズエネルギー変化によれば, が負,
が負, が正の場合には,
が正の場合には,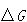 は負である.
は負である.
(5.1〜2)の条件を考えると,一定温度,一定圧力の条件下で変化の可能性について次のようにまとめることができる.
 (5.5)
(5.5)
系の平衡状態とは,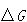 < 0の自発的な変化がこれ以上起こらなくなり,
< 0の自発的な変化がこれ以上起こらなくなり,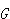 が最小となる状態である.
が最小となる状態である.
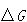 を活用すれば,異なる相が共存する相平衡や正方向と逆方向の化学反応が釣り合う化学平衡の条件を定めることができる.
を活用すれば,異なる相が共存する相平衡や正方向と逆方向の化学反応が釣り合う化学平衡の条件を定めることができる.
●ギブズエネルギーの物理的意義
ギブズエネルギーは,エネルギーという名称を使っているが,それはエネルギーのような保存関数ではない.
系と外界の圧力が等しい場合,系のエンタルピー変化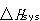 と外界のそれ
と外界のそれ とは大きさが等しく符号が反対の対応関係にある.
とは大きさが等しく符号が反対の対応関係にある.
しかし,そのような対応関係は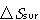 には成立しない.
には成立しない.
したがって,  においても外界との対応関係は成立しない.
においても外界との対応関係は成立しない.
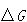 はエネルギーの次元をもっているが,いわゆる力学的なエネルギーとは違った意味をもっている.
はエネルギーの次元をもっているが,いわゆる力学的なエネルギーとは違った意味をもっている.
ギブズエネルギーは,かつてはギブズの自由エネルギーまたギブズ関数と呼ばれたこともある.
ギブズエネルギー変化を少し詳細に調べてみよう.温度,圧力一定の条件では
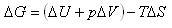 (5.6)
(5.6)
で,熱力学第一法則によれば
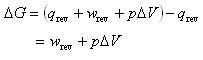 (5.7)
(5.7)
となる.
右辺は,可逆変化でなす仕事から系の膨張によってなす仕事を差し引いたものである.
系の変化にともなって系が外界の圧力に抗して膨張ずる仕事を除いた系のなし得る最大仕事がギブズエネルギー変化である.
すなわち,ギブズエネルギー変化は,
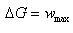 (5.8)
(5.8)
となり,系が一定温度,一定圧力の下でエネルギーを有効な仕事として移動させる能力の最大値を意味する.
●ギブズエネルギー変化と電位差
系の状態変化にともなう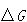 を直接測定するのには困難がある.
を直接測定するのには困難がある.
何故なら,大抵の場合,測定できる仕事は最大仕事よりも小さい.
しかし,ギブズエネルギー変化を「仕事をなし得る潜在的能力(potentiality)」とすれば,それを電位(electric potential)として定義できる.
すると,ある種の化学変化の始状態と終状態のギブズエネルギーの差は,電位差として測定することができる.
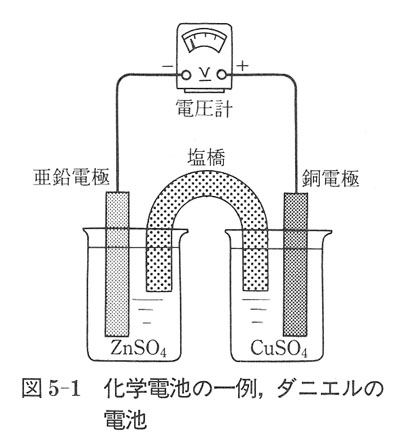 二つの電極反応を組み合わせた化学電池の例を図5-1に示した.この電池は,銅電極反応と亜鉛電極反応との組み合わせからできている.
二つの電極反応を組み合わせた化学電池の例を図5-1に示した.この電池は,銅電極反応と亜鉛電極反応との組み合わせからできている.
その電位差は電流を流すことなく測定することができる.正極,負極での反応は,
 (5.9)
(5.9)
で全体の反応は
 (5.10)
(5.10)
である.
ここで,硫酸銅と硫酸亜鉛水溶液を塩橋(salt bridge)で結んであるが,これは正負イオンの移動速度の差を生じないよう塩化カリウムの濃厚溶液をゼラチンで固めたもので,二つの溶液を電気的に接続するものである.
電池反応で可能な仕事の大きさは,電位差 と移動した電荷の総量
と移動した電荷の総量 との積に等しい.
との積に等しい.
物質1モルの電極反応によって生ずる電気エネルギーは
 (5.11)
(5.11)
である.
 はボルト(V)の単位で表した電位差で,
はボルト(V)の単位で表した電位差で, はファラデー定数,
はファラデー定数,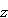 は物質1モルの反応で移動する電子のモル数である.
は物質1モルの反応で移動する電子のモル数である.
(5.10)の電極反応の場合の は1.10 Vであるので,
は1.10 Vであるので,
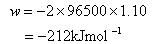
である.
これが,この電池反応のギブズエネルギー変化に相当する.すなわち,
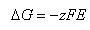 (5.12)
(5.12)
である.
銅-亜鉛電池反応の場合,反応エンタルピーは熱量測定によって

となっている.
すると

である.
反応が一定温度で起こり,最大仕事がなされたとすると,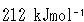 の仕事がなされ,残りの
の仕事がなされ,残りの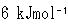 は熱として移動する.
は熱として移動する.
その結果,系のエントロピーは だけ減少する.
だけ減少する.
反応が可逆的に行われれば,外界のエントロピーは同じ大きさだけ増加し,系と外界の全体のエントロピーは変化しない.
一方,反応が不可逆的に起これば,外界のエントロピー増分は最大で を温度で割った
を温度で割った となる.
となる.
系のエントロピーの減少に変化がないので,系と外界の全体のエントロピーは大きく増加する.
つまり,反応の実現可能性が大きい.
全エントロピー変化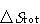 が正であることは,
が正であることは,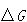 が負という事実から導かれる.
が負という事実から導かれる.
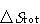 の方が化学変化の実現可能性を判断する上で明解であろうが,
の方が化学変化の実現可能性を判断する上で明解であろうが,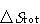 は反応の起こる道すじによってその値が変わるので,そのとり扱いが難しい.
は反応の起こる道すじによってその値が変わるので,そのとり扱いが難しい.
これに対して,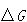 は系だけに注目し,反応の経路によらないので,
は系だけに注目し,反応の経路によらないので,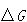 は反応の実現可能性を判断するパラメーターとして適当である.
は反応の実現可能性を判断するパラメーターとして適当である.
 平衡状態は,物質の状態変化の自発的な不可逆過程がこれ以上起こらない状態である.
平衡状態は,物質の状態変化の自発的な不可逆過程がこれ以上起こらない状態である. (5.1)
(5.1)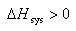 (5.2)
(5.2) は正で不都合であるが,
は正で不都合であるが, は正で条件を満たしている.
は正で条件を満たしている. で都合が良いが,
で都合が良いが,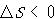 で不都合である.
で不都合である.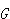 と呼ばれている.
と呼ばれている.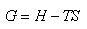 (5.3)
(5.3)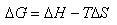 (5.4)
(5.4)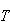 を
を に掛けたのは,単位をエネルギーの次元に統一するためである.
に掛けたのは,単位をエネルギーの次元に統一するためである. が負,
が負, が正の場合には,
が正の場合には,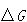 は負である.
は負である. (5.5)
(5.5)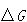 < 0の自発的な変化がこれ以上起こらなくなり,
< 0の自発的な変化がこれ以上起こらなくなり,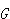 が最小となる状態である.
が最小となる状態である.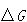 を活用すれば,異なる相が共存する相平衡や正方向と逆方向の化学反応が釣り合う化学平衡の条件を定めることができる.
を活用すれば,異なる相が共存する相平衡や正方向と逆方向の化学反応が釣り合う化学平衡の条件を定めることができる.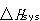 と外界のそれ
と外界のそれ とは大きさが等しく符号が反対の対応関係にある.
とは大きさが等しく符号が反対の対応関係にある.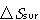 には成立しない.
には成立しない. においても外界との対応関係は成立しない.
においても外界との対応関係は成立しない.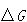 はエネルギーの次元をもっているが,いわゆる力学的なエネルギーとは違った意味をもっている.
はエネルギーの次元をもっているが,いわゆる力学的なエネルギーとは違った意味をもっている.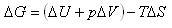 (5.6)
(5.6)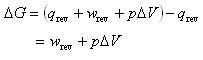 (5.7)
(5.7)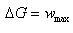 (5.8)
(5.8)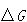 を直接測定するのには困難がある.
を直接測定するのには困難がある. 二つの電極反応を組み合わせた化学電池の例を図5-1に示した.この電池は,銅電極反応と亜鉛電極反応との組み合わせからできている.
二つの電極反応を組み合わせた化学電池の例を図5-1に示した.この電池は,銅電極反応と亜鉛電極反応との組み合わせからできている. (5.9)
(5.9) (5.10)
(5.10) と移動した電荷の総量
と移動した電荷の総量 との積に等しい.
との積に等しい. (5.11)
(5.11) はボルト(V)の単位で表した電位差で,
はボルト(V)の単位で表した電位差で, はファラデー定数,
はファラデー定数,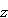 は物質1モルの反応で移動する電子のモル数である.
は物質1モルの反応で移動する電子のモル数である. は1.10 Vであるので,
は1.10 Vであるので,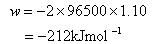
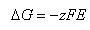 (5.12)
(5.12)

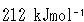 の仕事がなされ,残りの
の仕事がなされ,残りの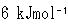 は熱として移動する.
は熱として移動する. だけ減少する.
だけ減少する. を温度で割った
を温度で割った となる.
となる.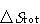 が正であることは,
が正であることは,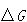 が負という事実から導かれる.
が負という事実から導かれる.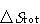 の方が化学変化の実現可能性を判断する上で明解であろうが,
の方が化学変化の実現可能性を判断する上で明解であろうが,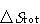 は反応の起こる道すじによってその値が変わるので,そのとり扱いが難しい.
は反応の起こる道すじによってその値が変わるので,そのとり扱いが難しい.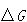 は系だけに注目し,反応の経路によらないので,
は系だけに注目し,反応の経路によらないので,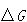 は反応の実現可能性を判断するパラメーターとして適当である.
は反応の実現可能性を判断するパラメーターとして適当である.