3.化学平衡
●気相反応の化学平衡
温度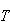 の下で進行する化学反応のギブズエネルギー変化は,生成系の化学ポテンシャルの総和から反応系のそれを引いたものである.
の下で進行する化学反応のギブズエネルギー変化は,生成系の化学ポテンシャルの総和から反応系のそれを引いたものである.
すなわち,
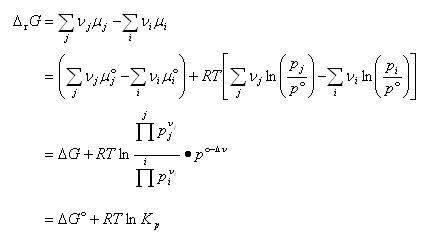 (5.22)
(5.22)
ここで,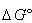 は反応の標準ギブズエネルギー変化,
は反応の標準ギブズエネルギー変化,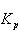 は圧平衡定数で,
は圧平衡定数で,
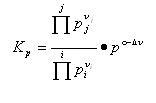 (5.23)
(5.23)
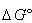 は反応のモル数変化で
は反応のモル数変化で
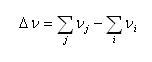 (5.24)
(5.24)
である.
正反応と逆反応の速度の釣り合った平衡状態では,
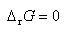 (5.25)
(5.25)
である.すると,圧平衡定数は
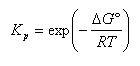 (5.26)
(5.26)
となる.
われわれは,どんな反応でも反応に関与する化学種の標準ギブズエネルギーが与えられれば,平衡定数を定めることができる.
圧平衡定数は,平衡反応に関係する化学種の分圧の関数で定義されている.分圧と濃度の間には
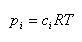 (5.27)
(5.27)
の関係がある.
したがって,濃度平衡定数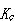 と圧平衡定数
と圧平衡定数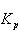 との間には,
との間には,
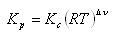 (5.28)
(5.28)
の関係がある.
ここで,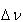 は(5.24)式で定義したモル数の変化である.反応によってモル数変化がない場合,
は(5.24)式で定義したモル数の変化である.反応によってモル数変化がない場合,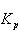 と
と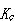 は等しい.
は等しい.
●ル・シャトリエの原理
平衡状態にある系の温度,圧力などの状態変数を変化させると,新しい平衡状態へ向かって平衡の移動が起こる.
その方向を定性的に示したものが平衡移動の法則であり,ル・シャトリエ(H.L. Le Chatelier)が1884年に提出したので,ル・シャトリエの原理といわれる.
その表現は「平衡にある系の状態変数の一つに変化を与えると,その変化によって生ずる影響をなるべく小さくする方向に平衡は移動する」である.
平衡系の圧力を高くすると,モル数の減少,つまり,体積の減少が起こる方向へ平衡は移動する.
また,温度を高くすると,熱の吸収が起こる方向に平衡は移動する.この原理は,熱力学第二法則によって基礎づけられている.
●気相反応の化学平衡の例 その1
簡単な例として四酸化二窒素の解離平衡
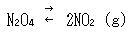 (5.29)
(5.29)
を調べよう.
N2O4は無色の気体であるが,常温・常圧で一部分が解離して褐色の二酸化窒素NO2を生ずる.
N2O4が平衡状態で解離する割合を解離度αという.平衡状態におけるN2O4とNO2の混合気体の全圧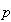 をとすると,平衡関係は下記のようになる.
をとすると,平衡関係は下記のようになる.
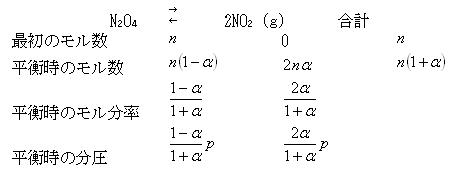
したがって,圧平衡定数は
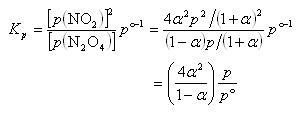 (5.30)
(5.30)
となる.
解離度αの圧力による変化は
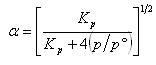 (5.31)
(5.31)
となる.
この式によれば,一定温度で全圧を大きくすると解離度は小さくなる.
つまり,平衡はN2O4側,モル数の減少する方向へ移動する.
この変化は,ル・シャトリエの原理から期待される通りである.
この反応は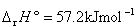 の吸熱反応である.
の吸熱反応である.
したがって,温度が高いと吸熱反応の起こる側へ平衡が移動し,逆に,低温では右側へ移動する.
反応のギブズエネルギー変化は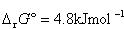 で,
で,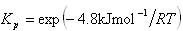 であるから常温付近の小さい温度変化で平衡定数が大きく変動する.
であるから常温付近の小さい温度変化で平衡定数が大きく変動する.
●平衡定数の温度変化
圧平衡定数の(5.26)式の対数をとると,
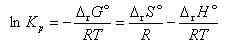 (5.32)
(5.32)
となる.
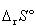 や
や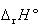 は温度によって変動するがその変化はそれ程大きいものではない.
は温度によって変動するがその変化はそれ程大きいものではない.
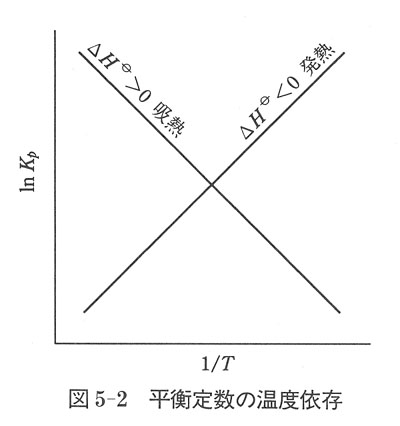
すると,反応エンタルピーの正負,反応が発熱か吸熱かによって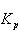 の温度依存性が違ってくる.
の温度依存性が違ってくる.
図5-2に示したように,吸熱反応では温度の上昇とともに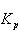 は大きくなり,発熱反応ではその逆である.
は大きくなり,発熱反応ではその逆である.
厳密には,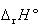 の温度変化を考えねばならないが,いろいろな温度での
の温度変化を考えねばならないが,いろいろな温度での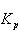 の測定によって反応エンタルピーのおよその値を定めることができる.
の測定によって反応エンタルピーのおよその値を定めることができる.
●気相反応の化学平衡の例 その2
化学熱力学は,化学合成の可能性を予言するための基礎を与えるものであるが,中でも空中窒素固定,アンモニア合成技術の確立程,大きな影響を与えたものはない.
窒素は植物の成長に欠かすことのできない肥料のもっとも重要な成分であり,ニトロ化合物は爆薬として大量の需要があった.
それにもかかわらず,19世紀までは,窒素源はチリ硝石とガスエ場やコークス炉からの副生アンモニアしかなかった.
したがって,大気中の窒素を利用することが緊急の課題であった.
20世紀の初めにドイツの化学者ハーバー(F. Haber)はネルンストの示唆をうけて窒素と水素からアンモニアを合成する基礎研究を行った.
アンモニア生成反応は
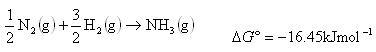 (5.33)
(5.33)
で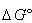 < 0であるからアンモニア合成は可能である.
< 0であるからアンモニア合成は可能である.
しかし,この反応は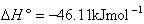 の発熱反応であるからル・シャトリエの原理から低い温度の方が合成に有利である.
の発熱反応であるからル・シャトリエの原理から低い温度の方が合成に有利である.
また,全圧を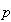 とし,生成NH3のモル分率を
とし,生成NH3のモル分率を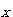 とすると,N2,H2のモル分率はそれぞれ ,
とすると,N2,H2のモル分率はそれぞれ ,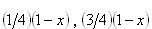 である.
である.
したがって,圧平衡定数は
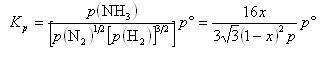 (5.34)
(5.34)
である.
一定温度で,x≪1のときxはpに比例し,高い圧力の方が合成に有利である.
工業的にアンモニアを合成するには,圧力200〜1000atm,温度400〜500℃とし,反応速度を大きくするため四酸化三鉄を主体とする触媒(15章参照)が用いられる.
このような高温,高圧の化学合成の技術を確立するためには幾多の困難があった.
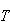 の下で進行する化学反応のギブズエネルギー変化は,生成系の化学ポテンシャルの総和から反応系のそれを引いたものである.
の下で進行する化学反応のギブズエネルギー変化は,生成系の化学ポテンシャルの総和から反応系のそれを引いたものである.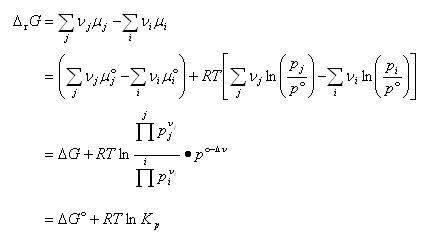 (5.22)
(5.22)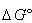 は反応の標準ギブズエネルギー変化,
は反応の標準ギブズエネルギー変化,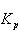 は圧平衡定数で,
は圧平衡定数で,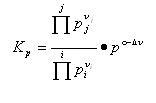 (5.23)
(5.23)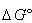 は反応のモル数変化で
は反応のモル数変化で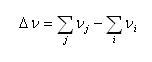 (5.24)
(5.24)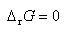 (5.25)
(5.25)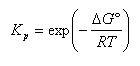 (5.26)
(5.26)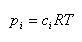 (5.27)
(5.27)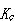 と圧平衡定数
と圧平衡定数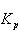 との間には,
との間には,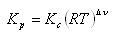 (5.28)
(5.28)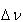 は(5.24)式で定義したモル数の変化である.反応によってモル数変化がない場合,
は(5.24)式で定義したモル数の変化である.反応によってモル数変化がない場合,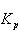 と
と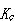 は等しい.
は等しい.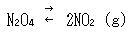 (5.29)
(5.29)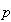 をとすると,平衡関係は下記のようになる.
をとすると,平衡関係は下記のようになる.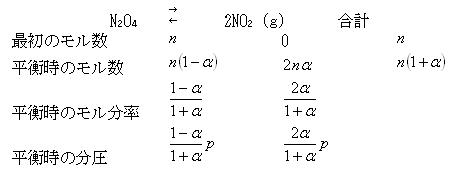
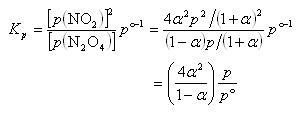 (5.30)
(5.30)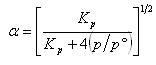 (5.31)
(5.31)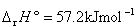 の吸熱反応である.
の吸熱反応である.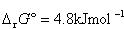 で,
で,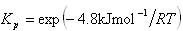 であるから常温付近の小さい温度変化で平衡定数が大きく変動する.
であるから常温付近の小さい温度変化で平衡定数が大きく変動する.
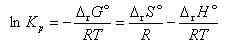 (5.32)
(5.32)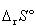 や
や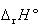 は温度によって変動するがその変化はそれ程大きいものではない.
は温度によって変動するがその変化はそれ程大きいものではない.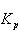 の温度依存性が違ってくる.
の温度依存性が違ってくる.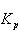 は大きくなり,発熱反応ではその逆である.
は大きくなり,発熱反応ではその逆である.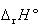 の温度変化を考えねばならないが,いろいろな温度での
の温度変化を考えねばならないが,いろいろな温度での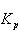 の測定によって反応エンタルピーのおよその値を定めることができる.
の測定によって反応エンタルピーのおよその値を定めることができる.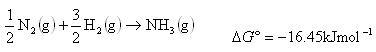 (5.33)
(5.33)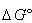 < 0であるからアンモニア合成は可能である.
< 0であるからアンモニア合成は可能である.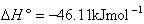 の発熱反応であるからル・シャトリエの原理から低い温度の方が合成に有利である.
の発熱反応であるからル・シャトリエの原理から低い温度の方が合成に有利である.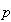 とし,生成NH3のモル分率を
とし,生成NH3のモル分率を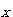 とすると,N2,H2のモル分率はそれぞれ ,
とすると,N2,H2のモル分率はそれぞれ ,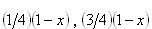 である.
である.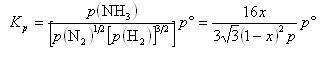 (5.34)
(5.34)