2.一成分系の相平衡
●一成分系の相律
相律を一成分系に適用するとC = 1であるから自由度は
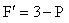 (6.5)
(6.5)
である.
つまり
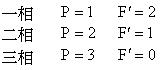
である.
一相の場合,二つの示強性状態変数を自由に選ぷことができる.
状態変数として,温度T,圧力P,モル体積Vmを選ぶとその間には,
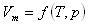 (6.6)
(6.6)
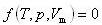 (6.7)
(6.7)
のような関係式が成立する.
たとえば,気体では,圧力零の極限で理想気体の状態方程式
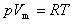 (6.8)
(6.8)
が成立する.
一成分系では,自由度が最大2であるから,二つの示強性状態変数を座標軸にとって相の間の平衡関係を図示できる.
二つの状態変数として普通は温度と圧力を選ぶ.このような図を相状態図または単に状態図と呼ぶ.
●二相平衡−クラペイロンークラウジウスの式
固相−液相,液相−気相などの二つの相が共存する場合,(6.5)式より自由度は一つになる.
つまり,圧力を指定すれば,二相共存の温度は指定される.二相平衡の圧力と温度の関係を考えてみよう.
相αと相βが共存する平衡条件は,温度T,圧力pが各相において等しいことと二つの相の化学ポテンシャルが等しいことである.
すなわち,
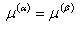 (6.9)
(6.9)
である.
いま,相平衡を保ったまま, のように温度変化
のように温度変化 のために圧力変化
のために圧力変化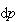 が起こったとする.
が起こったとする.
平衡条件は,
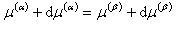 (6.10)
(6.10)
である.
(6.9)式を考えると,
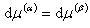 (6.11)
(6.11)
となる.
μはモル当りのギブズエネルギーで,ギブズエネルギーの微小変化は前章で学んだので,それを応用すると
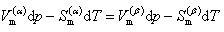 (6.12)
(6.12)
の式が導かれる.
ここで添字のmはモル当りの状態量を示す.
この式より
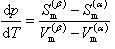 (6.13)
(6.13)
となる.
ここで,α→βの相変化にともなうエントロピー変化は転移エンタルピー を温度Tで割ったものであるから
を温度Tで割ったものであるから
 (6.14)
(6.14)
となる.
この式をクラペイロン−クラウジウスの式といい,二相平衡の際の圧力と温度の関係を示すものである.
固体から液体へ変化するときの体積変化は小さいので,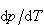 の値は大きな値となる.
の値は大きな値となる.
つまり,固相と液相の共存する圧力−温度の曲線は,小さな温度変化に対して大きな圧力変化をともなう.
液体と気体が平衡的に存在する場合,気体のモル体積は液体のそれに比べて非常に大きい.
したがって,液体のモル体積を無視できる.
(6.14)式は
 (6.15)
(6.15)
となり,理想気体の方程式を適用すると
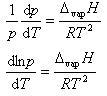 (6.16)
(6.16)
が得られる.
蒸発エンタルピーが温度によって変化しないという仮定の下で(6.16)式を積分すると
 (6.17)
(6.17)
となる.
図6-1にいくつかの物質の蒸気圧の対数を1/Tに対してプロットした.
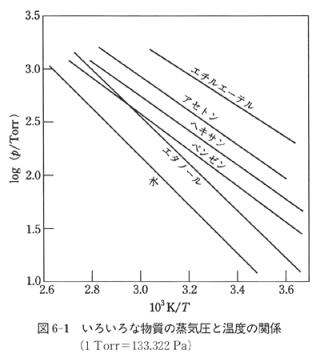
それらはほぼ直線となっており,この直線の勾配は となっている.
となっている.
蒸発エンタルピーの大きい水とエタノールの勾配は大きくなっている.
固相と気相の平衡についても(6.16)式を適用することができる.その場合には,エンタルピー変化は昇華エンタルピー となる.
となる.
●三相平衡
固体,液体,気体の三相が共存する平衡では,自由度は零である.
したがって,物質によって温度,圧力は指定される.
この点を三重点という.
水の三重点は,273.16K(0.01℃),610.6 Pa(4.58 Torr)であって,この温度は第10回国際度量衡委員会総会で温度の唯一の定点と定め,その熱力学温度を273.16Kとした.
物質によっては,三重点で異なる結晶形の固体同士が平衡となる場合もある.
●臨界状態
液体と気体の相の区別は,ある圧力,温度以上で消失する.この点を臨界点と呼ぶ.
臨界点に相当する温度,圧力,モル体積を臨界温度,臨界圧力,臨界体積といい,それらは物質固有な定数である.
表6-1にいろいろな物質の臨界定数を与える.
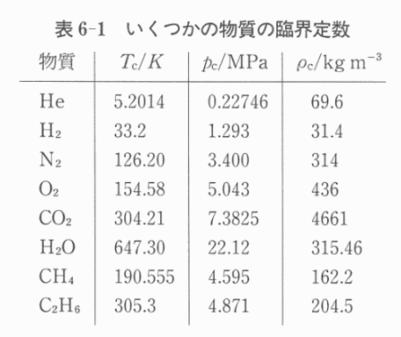
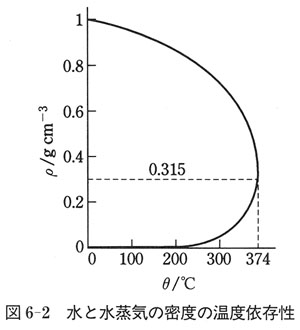
臨界状態がどんな状態であるかを理解するために,水の液体と気体が共存する場合の密度と温度の関係をプロットした図を図6-2に示す.
低い温度では,液体の密度の方が気体のそれよりもずっと大きい.
すなわち,液体の相と気体の相は,液体表面によって明瞭に区別されている.
しかし,高温度になると,気相の密度が大きくなり,液体の密度に近づく.臨界点の374℃では完全に等しくなり,それより高温では液体状態は存在しない.
図6-3には,水の蒸発エンタルピーを温度の関数でプロットした.蒸発エンタルピーは温度の上昇とともに減少する.
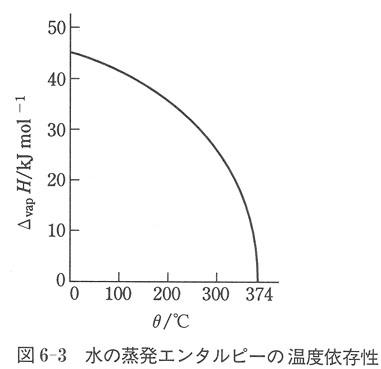
臨界点の374℃では,その値は零となる.
それは,それ以上の温度では液体の状態が存在しないことを意味している.
臨界状態がどのように定義されるかを説明するために,気体の圧力と体積の関係を二酸化炭素について図6-4に示す.

気体の圧力と体積の関係は,理想気体に近い条件ではある一定温度で双曲線となる.
このようなp - Vの関係を示す曲線を等温線という.
温度が低下すると等温線が双曲線からだんだんずれる.そして,変曲点をもつようになる.
すなわち,
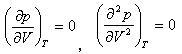 (6.18)
(6.18)
を満たす.
この点が臨界点である.
この点以下の温度では,あるモル体積まで圧縮すると液体が析出し始め,体積に対して圧力は一定となる.
つまり,気体と液体が共存する.
さらに,圧縮をするとすべてが液体となった点から急激に圧力が上昇する.
臨界点は,気体の状態方程式より(6.18)式を用いて求めることができる.
臨界温度の高い物質は分子間力が比較的強い.
一方,希ガス原子のように原子間力が弱い場合には,臨界温度は非常に低いものとなる.
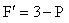 (6.5)
(6.5)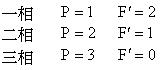
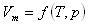 (6.6)
(6.6)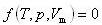 (6.7)
(6.7)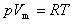 (6.8)
(6.8)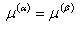 (6.9)
(6.9) のように温度変化
のように温度変化 のために圧力変化
のために圧力変化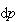 が起こったとする.
が起こったとする.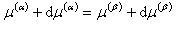 (6.10)
(6.10)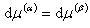 (6.11)
(6.11)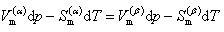 (6.12)
(6.12)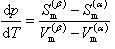 (6.13)
(6.13) を温度Tで割ったものであるから
を温度Tで割ったものであるから (6.14)
(6.14)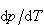 の値は大きな値となる.
の値は大きな値となる. (6.15)
(6.15)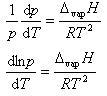 (6.16)
(6.16) (6.17)
(6.17)
 となっている.
となっている. となる.
となる.



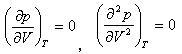 (6.18)
(6.18)