格子欠陥を無視すると,ω(Cu) + ω(Zn) = 1となる.
室温ではω(Cu) = 1,ω(Zn) = 0であるが,昇温するにつれω(Cu)は減少し,ω(Zn)は増加する.
β黄銅は460℃で相転移を示し,この温度以上ではω(Cu) =ω(Zn) = 0.5となる.ここで占有の様子を表すパラメーターηを
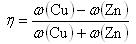
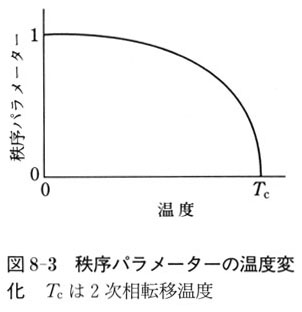
で定義すると,ηは図8-3に示したように1から0の間の値をとり,秩序の度合いを表していることがわかる.
これを秩序度といい(秩序パラメーターともいう),2次相転移に特徴的な指標である.
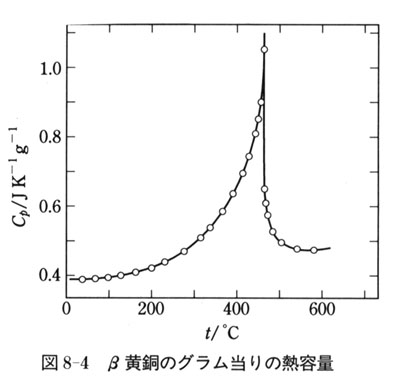
図8-4はβ黄銅の熱容量であるが,1次相転移と異なり,かなり広い温度領域にわたって相転移が起こっていることがわかる.
●相転移の分類
自然界には様々な相転移が存在する.
一つの試みとして,表8-1に相転移の分類を示した.

典型的な相転移は秩序・無秩序型相転移である.
分子やイオンが結晶中で乱雑に向き(配向という)を変えることによる相転移である.
配向無秩序結晶(あるいは柔粘性結晶)や液晶の転移がこれに対応する.
上に示した2元合金のように,原子や分子の位置に関する秩序・無秩序転移もこれに属する.
磁性体では温度が高いとスピンの配向がランダムな常磁性であるが,低温にすると熱運動による撹乱が減少し,強磁性や反強磁性状態に整列する.
変位型相転移もよく知られている.
これは原子やイオンの位置が変位することによる相転移であり,対称性の低い低温相での配置から対称性の高い高温相へ転移するものである.
主として強誘電体や反強誘電体でみられる.
量子効果によって生ずるマクロな相転移現象の例として,液体ヘリウムでみられる超流動転移や,電気抵抗がゼロになる超伝導転移がある.
一般に分子内の化学結合エネルギーは分子間相互作用エネルギーよりもはるかに大きい.
したがって相転移が起こって分子の環境が変わったくらいでは,分子内エネルギーは影響を受けないものである.
言い換えると,相転移の前後で分子の形は変わらないのが普通である.
ところが近年,電子が直接的に関与する相転移が幾つか報告され,大きな注目を集めている.
電子が関与するということは,分子の電子状態も影響を受けることになり,可視・紫外吸収スペクトルに著しい変化が現れる.
ひいては分子の形が変わり,結晶の色も変化することになる.
表8-1に示したように,その代表例はスピンクロスオーバー現象である.
これは遷移金属錯体の電子スピンの状態が結晶を加熱することにより低スピンから高スピンになる現象である.
同じ遷移金属イオンでありながら不対電子の数が少ないとき,スピン量子数は小さくなり低スピンと呼ばれる.
不対電子数が多い状態を高スピンという.スピン量子数の変化は,温度による熱誘起ばかりではなく,圧力や光による誘起も見出されている.
混合原子価現象というのは一つの化学式あるいは分子中に,酸化数の異なる元素が共存することを意味し,たとえば磁鉄鉱Fe3O4では2個のFe(Ⅲ)と1個のFe(Ⅱ)から成っている.
混合原子価化合物として注目を集めているのは鉄の三核錯体[Fe(Ⅲ)2 Fe(Ⅱ)]や二核錯体[Fe(Ⅲ) Fe(Ⅱ)]である.
Fe(Ⅱ)はFe(Ⅲ)より電子が一つ多いので,[Fe(Ⅲ)2 Fe(Ⅱ)]という錯体は[Fe(Ⅲ)3 + 1電子]とみなせる.
低温で特定の原子上に局在していたこの電子が,相転移により分子内の鉄原子上を飛び移るため,鉄の原子価が時間的に変動ずる珍しい現象である.
パイエルス転移というのは,1次元的な相互作用が強い電気の1次元導体結晶を冷却すると,転移温度よりも低温側で絶縁体になる相転移,すなわち非金属・金属転移である.
サーモクロミズムとは,温度変化により物質の色が変化する現象であり,分子の電子状態の変化に対応する.
サーモクロミズムを起こす原因にはいろいろあるが,遷移金属錯体では,配位構造が変わったり,配位数そのものが変化することが原因となっている.
たとえば,2価のニッケルイオンを中心金属元素とする錯体は,平面四配位の時は緑色の反磁性化合物だが,四面体配位になると褐色の常磁性化合物となる.
有機化合物の中には電子を放り出そうとする傾向が強い電子供与体(ドナー : D)と電子を受け入れやすい電子受容体(アクセプター : A)が存在する.
これら両者から成る結晶では多くの場合DからAに電子が移動し[D+ A-]という電荷移動錯体が形成される.
ところが,ある種の化合物では,室温でほんのわずかしか電荷移動が起こらないのに,低温で相転移を起こし,より多くの電荷が移動する例が見出され,中性・イオン性転移として興味がもたれている.
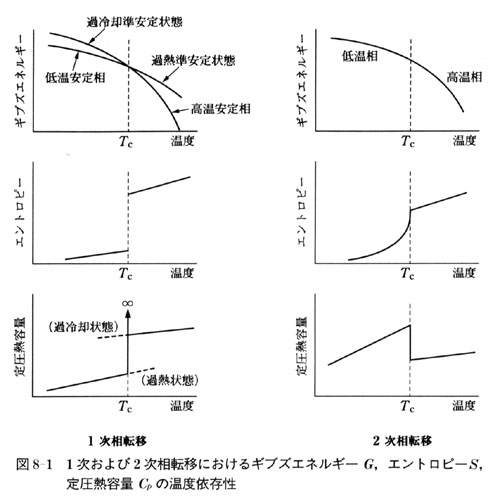
●相転移における熱力学量の変化
さて,相転移の研究から何が分かるかを考えてみよう.
相転移近傍で熱容量はピークを示したり,飛びを示したりする.
もし相転移が起こらなければこうなるであろうと予想される正常熱容量曲線を何らかの方法で算出すると,実測値と正常値の差,すなわち過剰熱容量ΔCpが相転移に基づく寄与である.

熱容量の定義に立ち帰ると,転移に基づくエンタルピーの増分
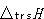 とエントロピーの増分
とエントロピーの増分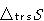 が次の関係式より求められる.
が次の関係式より求められる.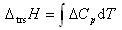 (8.4)
(8.4)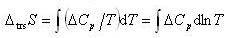 (8.5)
(8.5)他方,エネルギー的に等価なミクロな状態数WとマクロなエントロピーSの間にはボルツマンの原理により
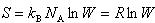
の関係が成り立つ.
ここでkBはボルツマン定数,NAはアボガドロ定数,Rは気体定数である.
相転移エントロピー
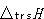 は,高温相と低温相のエントロピーの差に対応するので,
は,高温相と低温相のエントロピーの差に対応するので,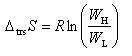 (8.6)
(8.6)となる.
ここでWHとWLは高温相と低温相でのミクロな状態数である.
低温相が秩序相の場合にはWL = 1なので,転移エントロピーの実測値から高温相で幾通りのミクロな状態が存在するかを推定することができる.
転移エンタルピー
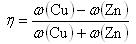 は,相転移前後での分子間相互作用のエネルギー差を表している.
は,相転移前後での分子間相互作用のエネルギー差を表している.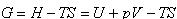 なので
なので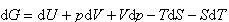 である.
である.
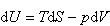 やdVを適用すると
やdVを適用すると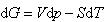 なので,Gの温度Tおよび圧力pに関する1次微分は
なので,Gの温度Tおよび圧力pに関する1次微分は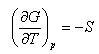 (8.1)
(8.1)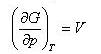 (8.2)
(8.2)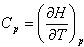 であり
であり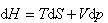 なので
なので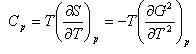 (8.3)
(8.3)