

Next: 演習問題2解答
Up: 目次
Previous: 目次
次のそれぞれの正誤を判定しなさい。
問題1−1
関数
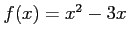 について,
について,
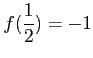 である.
である.
解答 誤
コメント
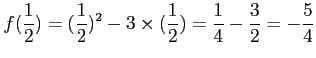
問題1−2
関数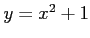 と関数
と関数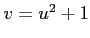 は同じ関数である.
は同じ関数である.
解答 正
コメント これらはともに、数を2乗して1を加えるという関数であり、用いる変数記号が異なるだけで関数としては同じものである。
問題1−3
関数
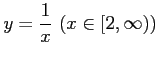 の値域は
の値域は
![$ [0,\displaystyle \frac{1}{2}]$](img7.png) である.
である.
解答 誤
コメント 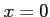 は値域に入らない。値域は
は値域に入らない。値域は
![$ (0,\displaystyle \frac{1}{2}]$](img9.png) である。
である。
問題1−4
関数
![$ y=x^{2} (x\in[-1,3])$](img10.png) の値域は
の値域は![$ [1,9]$](img11.png) である.
である.
解答 誤
コメント
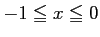 のとき、
のとき、
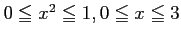 のとき、
のとき、
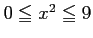 だから、値域は
だから、値域は![$ [0,9]$](img15.png) である。
である。
問題1−5
関数
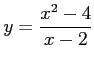 と関数
と関数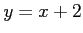 は同じ関数である.
は同じ関数である.
解答 誤
コメント 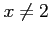 のとき、
のとき、
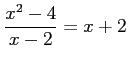 だが、
だが、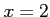 のとき、
のとき、
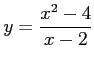 は定義されていない。
は定義されていない。
一方、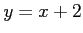 はすべての実数
はすべての実数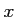 で定義されている。定義域が違うのでこの2つは異なる関数である。
で定義されている。定義域が違うのでこの2つは異なる関数である。
問題1−6
関数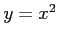 は1対1であり,逆関数が存在する.
は1対1であり,逆関数が存在する.
解答 誤
コメント 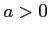 のとき、
のとき、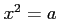 となるのは、
となるのは、
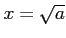 と
と
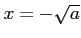 の2つであるので、1対1でない。したがって、逆関数は存在しない。
の2つであるので、1対1でない。したがって、逆関数は存在しない。
問題1−7
関数
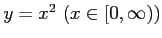 の逆関数は
の逆関数は
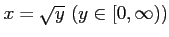 である.
である.
解答 正
問題1−8
関数
![$ y=x^{2} (x\in(-\infty,0])$](img29.png) の逆関数は
の逆関数は
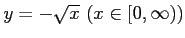 である.
である.
解答 正
コメント 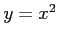 を
を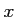 について解けば、
について解けば、
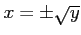 であるが、
であるが、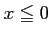 だから、逆関数は
だから、逆関数は
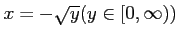 。変数をとり替えると、
。変数をとり替えると、
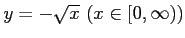 である.
である.
問題1−9
関数
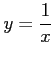 の逆関数は
の逆関数は
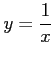 である.
である.
解答 正
コメント
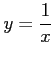 を
を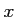 について解くと、
について解くと、
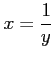 となるが、変数をとり替えると、
となるが、変数をとり替えると、
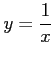 となる。
となる。
問題1−10
関数
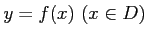 が1対1であるための必要十分条件は
が1対1であるための必要十分条件は
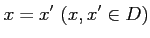 ならば
ならば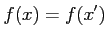 が成り立つことである.
が成り立つことである.
解答 誤
コメント 関数
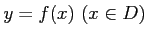 が1対1であるとは、
が1対1であるとは、
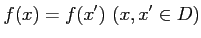 ならば
ならば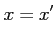 が成り立つことである。
が成り立つことである。
問題1−11
関数
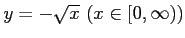 は狭義単調減少関数である.
は狭義単調減少関数である.
解答 正
コメント
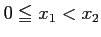 とすれば、
とすれば、
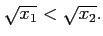 ゆえに、
ゆえに、
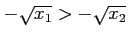 となり、狭義単調減少関数である。
となり、狭義単調減少関数である。
問題1−12
関数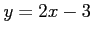 の逆関数は
の逆関数は
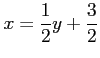 である.
である.
解答 正
コメント 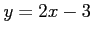 を
を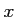 について解けば、
について解けば、
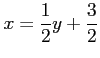 を得る。変数をとり替えて、
を得る。変数をとり替えて、
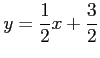 と表しても良い。
と表しても良い。


Next: 演習問題2解答
Up: 目次
Previous: 目次
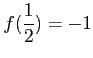 である.
である.
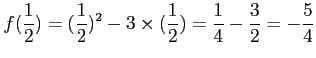
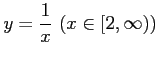 の値域は
の値域は
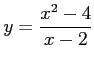 と関数
と関数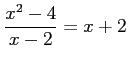 だが、
だが、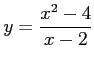 は定義されていない。
は定義されていない。
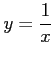 の逆関数は
の逆関数は
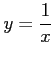 である.
である.
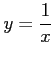 を
を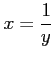 となるが、変数をとり替えると、
となるが、変数をとり替えると、
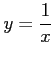 となる。
となる。
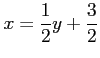 である.
である.
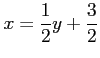 を得る。変数をとり替えて、
を得る。変数をとり替えて、
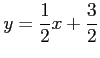 と表しても良い。
と表しても良い。