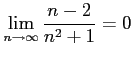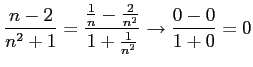Next: 演習問題3解答
Up: 目次
Previous: 演習問題1解答
次のそれぞれの正誤を判定しなさい。
問題2−1
実数の集合![$ A=(-3,4]$](img47.png) の上界の全体の集合は
の上界の全体の集合は
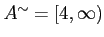 ,下界の全体の集合は
,下界の全体の集合は
![$ A_{\sim}=(-\infty,-3]$](img49.png) であるから,
であるから,
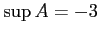 ,
,
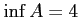 である.
である.
解答 誤
コメント 上限は最小の上界、下限は最大の下界だから、
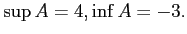
問題2−2
実数の集合
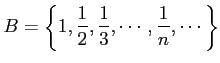 に対し,
に対し,
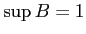 ,
,
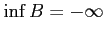 である.
である.
解答 誤
コメント
![$ B^{\sim}=[1,\infty), B_{\sim}=(-\infty,0] $](img56.png) だから、
だから、
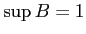 は正しいが、
は正しいが、
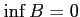 である。
である。
問題2−3
実数の集合
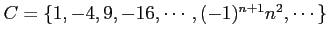 に対し,上界全体の集合は
に対し,上界全体の集合は
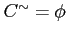 ,下界の全体の集合は
,下界の全体の集合は
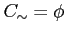 だから,
だから,
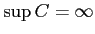 ,
,
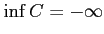 である.
である.
解答 正
コメント どんな実数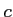 に対しても、十分大きな奇数
に対しても、十分大きな奇数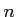 をとれば、
をとれば、
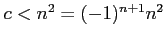 となり、十分大きな偶数をとれば、
となり、十分大きな偶数をとれば、
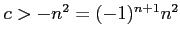 となるので、上界も下界も存在しない。
となるので、上界も下界も存在しない。
問題2−4
実数の集合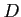 に最小値
に最小値
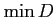 があれば
があれば
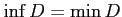 である.
である.
解答 正
コメント 最小値は最大の下界だからである。
問題2−5
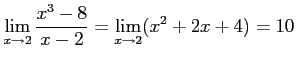
解答 誤
コメント
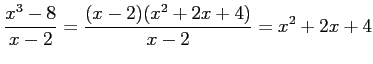 。極限値は
。極限値は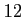 である。
である。
問題2−6
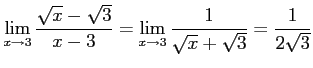
解答 正
コメント
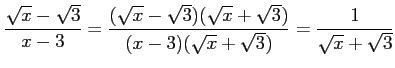
問題2−7
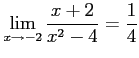
解答 誤
コメント
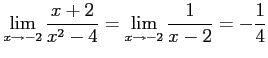
問題2−8
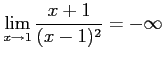
解答 誤
コメント
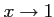 のとき、
のとき、
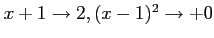 だから、
だから、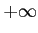 に発散する。
に発散する。
問題2−9
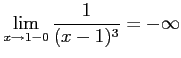
解答 正
コメント 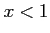 のとき、
のとき、
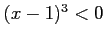 であるから、
であるから、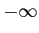 に発散する。
に発散する。
問題2−10
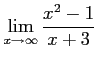 =
=
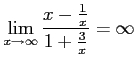
解答 正
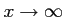 のとき、
のとき、
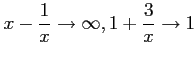 だからである。
だからである。
問題2−11
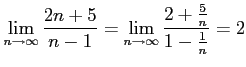
解答 正
コメント
 のとき、
のとき、
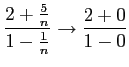 =
=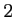
問題2−12
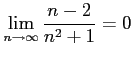
解答 正
コメント
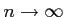 のとき、
のとき、
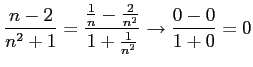
問題2−13
実数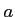 に対して,記号
に対して,記号![$ [a]$](img96.png) で
で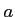 を超えない最大の整数とする.関数
を超えない最大の整数とする.関数![$ f(x)=[x]$](img97.png) は
は
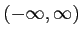 のすべての点で連続である.
のすべての点で連続である.
解答 誤
コメント 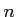 を整数とするとき、
を整数とするとき、
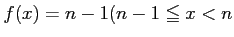 のとき
のとき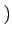 だから、
だから、
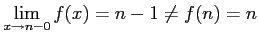 だから、
だから、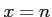 で連続でない。
で連続でない。



Next: 演習問題3解答
Up: 目次
Previous: 演習問題1解答
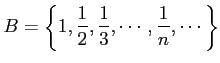 に対し,
に対し,
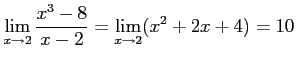
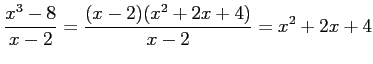 。極限値は
。極限値は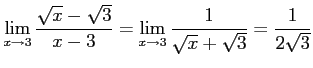
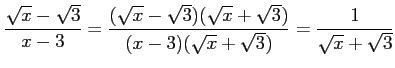
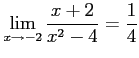
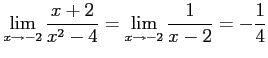
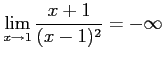
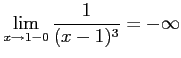
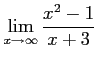 =
=
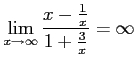
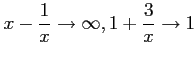 だからである。
だからである。
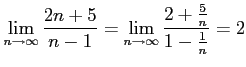
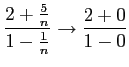 =
=