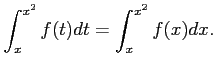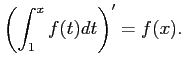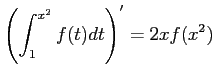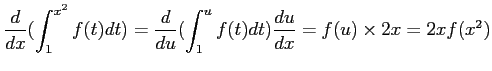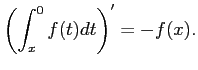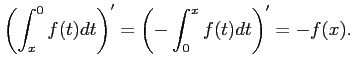

Up: 目次
Previous: 演習問題11解答
次のそれぞれの正誤を判定しなさい。
問題12−1
連続関数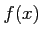 について,関数
について,関数 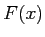 が
が
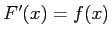 を満たすとき,
を満たすとき,
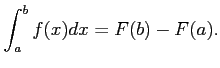
解答 正
問題12−2
![$\displaystyle \int_{1}^{2}x^{4}dx=\biggl{[}4x^{3}\biggr{]}_1^{2}=32-4=28.$](img389.png)
解答 誤
コメント
![$\displaystyle \int_{1}^{2}x^{4}dx=\biggl{[}\frac{x^{5}}{5}\biggr{]}_1^{2}=\frac{32}{5}-\frac{1}{5}=\frac{31}{5}.$](img390.png)
問題12−3
解答 誤
コメント
問題12−4
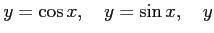 軸
軸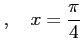 で囲む図形の面積
で囲む図形の面積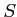 は
は
解答 正
問題12−5
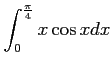 |
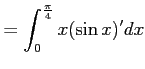 |
|
| |
![$\displaystyle =\biggl{[}x\sin x\biggr{]}_0^{\frac{pi}{4}}-\int_0^{\frac{\pi}{4}}\sin xdx$](img405.png) |
|
| |
![$\displaystyle =\dfrac{\pi}{4}\sin\dfrac{\pi}{4}+\biggl{[}\cos x\biggr{]}_0^{\frac{\pi}{4}}$](img406.png) |
|
| |
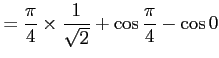 |
|
| |
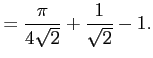 |
|
解答 正
問題12−6
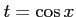 とおくと,
とおくと,
 であり,
であり,
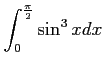 |
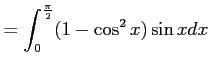 |
|
| |
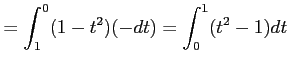 |
|
| |
![$\displaystyle =\biggl{[}\dfrac{t^3}{3}-t\biggr{]}_0^1=\dfrac{1}{3}-1=-\dfrac{2}{3}.$](img413.png) |
|
解答 誤
コメント
![$ \displaystyle \int_{1}^{0}(1-t^{2})(-dt)=\int_{0}^{1}(1-t^{2})dt=[t-\frac{t^{3}}{3}]_{0}^{1}=\frac{2}{3}$](img414.png)
問題12−7
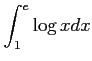 |
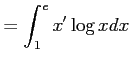 |
|
| |
![$\displaystyle =\biggl{[}x\log x\biggr{]}_1^e-\int_1^ex\times\dfrac{1}{x}dx$](img417.png) |
|
| |
![$\displaystyle =e\log e-\biggl{[}x\biggr{]}_1^e$](img418.png) |
|
| |
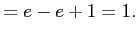 |
|
解答 正
問題12−8
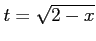 とおくと
とおくと 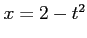 ,
,
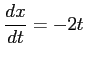 だから
だから
解答 誤
コメント 最後の等式は
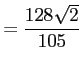 となる。
となる。
問題12−9
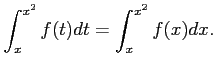
解答 正
コメント 右辺では積分区間の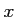 と関数の変数の
と関数の変数の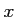 は別のものであるのに同じ記号
は別のものであるのに同じ記号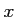 を用いているが、
を用いているが、
混同しないように右辺のように区別して書くことが勧められる。
問題12−10
連続関数 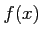 について
について
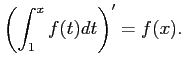
解答 正
問題12−11
連続関数 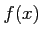 について
について
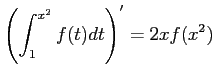
解答 正
コメント  とおくと、
とおくと、
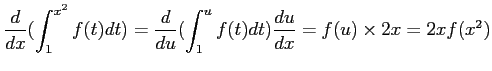
問題12−12
連続関数 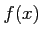 について
について
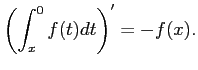
解答 正
コメント
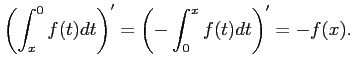


Up: 目次
Previous: 演習問題11解答
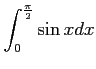
![$\displaystyle = \biggl{[}\cos x\biggr{]}_0^{\frac{\pi}{2}}$](img392.png)
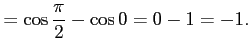
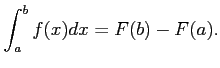
![$\displaystyle \int_{1}^{2}x^{4}dx=\biggl{[}4x^{3}\biggr{]}_1^{2}=32-4=28.$](img389.png)
![$\displaystyle \int_{1}^{2}x^{4}dx=\biggl{[}\frac{x^{5}}{5}\biggr{]}_1^{2}=\frac{32}{5}-\frac{1}{5}=\frac{31}{5}.$](img390.png)
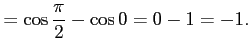
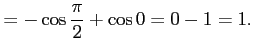
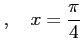 で囲む図形の面積
で囲む図形の面積![$\displaystyle =\int_0^{frac{\pi}{4}}(\cos x-\sin x)dx=\biggl{[}\sin x+\cos x\biggr{]}_0^{\frac{\pi}{4}}$](img400.png)
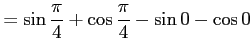
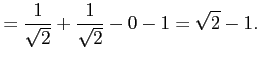
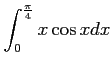
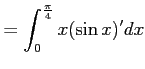
![$\displaystyle =\biggl{[}x\sin x\biggr{]}_0^{\frac{pi}{4}}-\int_0^{\frac{\pi}{4}}\sin xdx$](img405.png)
![$\displaystyle =\dfrac{\pi}{4}\sin\dfrac{\pi}{4}+\biggl{[}\cos x\biggr{]}_0^{\frac{\pi}{4}}$](img406.png)
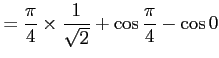
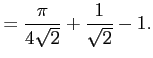
 であり,
であり,
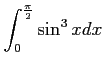
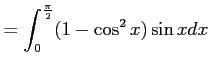
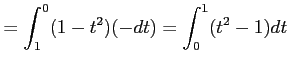
![$\displaystyle =\biggl{[}\dfrac{t^3}{3}-t\biggr{]}_0^1=\dfrac{1}{3}-1=-\dfrac{2}{3}.$](img413.png)
![$ \displaystyle \int_{1}^{0}(1-t^{2})(-dt)=\int_{0}^{1}(1-t^{2})dt=[t-\frac{t^{3}}{3}]_{0}^{1}=\frac{2}{3}$](img414.png)
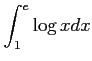
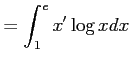
![$\displaystyle =\biggl{[}x\log x\biggr{]}_1^e-\int_1^ex\times\dfrac{1}{x}dx$](img417.png)
![$\displaystyle =e\log e-\biggl{[}x\biggr{]}_1^e$](img418.png)
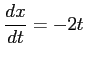 だから
だから
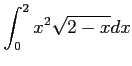
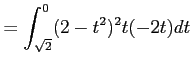
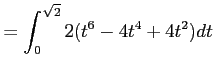
![$\displaystyle =2\biggl{[}\dfrac{t^7}{7}-\dfrac{4t^5}{5}+\dfrac{4t^3}{3}\biggr{]}_0^{\sqrt{2}}$](img426.png)
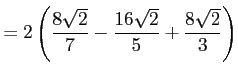
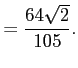
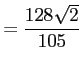 となる。
となる。