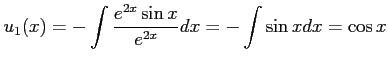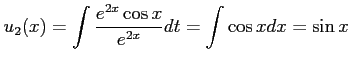

Next: 演習問題12解答
Up: 目次
Previous: 演習問題10解答
次のそれぞれの正誤を判定しなさい。
問題11−1
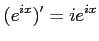
解答 正
コメント 一般に、複素数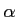 について、
について、
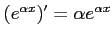 がなりたつ。
がなりたつ。
問題11−2
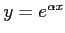 を線形微分方程式
を線形微分方程式
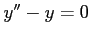 の解とすると
の解とすると
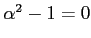 が成り立ち,
が成り立ち,
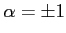 だから,
だから,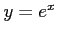 と
と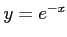 は解であり,
は解であり,
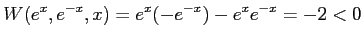 を満たし,1次独立な解である.
を満たし,1次独立な解である.
解答 正
問題11−3
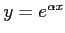 を2階線形微分方程式
を2階線形微分方程式
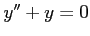 の解とすると,
の解とすると,
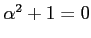 が成り立つ.
が成り立つ.
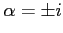 だから,
だから,
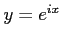 と
と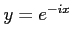 は
は
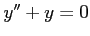 の解であり,
の解であり,
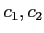 を定数とするとき
を定数とするとき
も
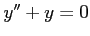 の解だから,
の解だから, と
と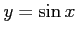 は
は
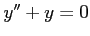 の解であるが,1次独立ではない.
の解であるが,1次独立ではない.
解答 誤
コメント 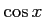 と
と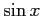 は互いに他方の定数倍ではないから1次独立である。
は互いに他方の定数倍ではないから1次独立である。
このことは、
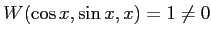 から判定することもできる。
から判定することもできる。
問題11−4
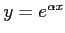 を2階線形微分方程式
を2階線形微分方程式
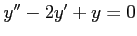 の解とすると
の解とすると
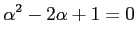 が成り立つ.この2次方程式の解は
が成り立つ.この2次方程式の解は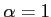 が重根である .したがって,
が重根である .したがって,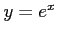 は微分方程式の解であるが,
は微分方程式の解であるが,
さらに,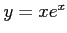 も微分方程式の解になっており,
も微分方程式の解になっており,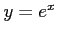 と
と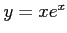 は1次独立である.
は1次独立である.
解答 正
コメント 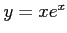 については、
については、
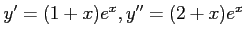 より、
より、
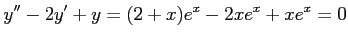 がなりたつから、解である。
がなりたつから、解である。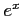 と
と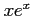 とは互いに他方の定数倍になっていないから1次独立である。
とは互いに他方の定数倍になっていないから1次独立である。
このことは、
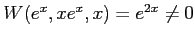 から判定することもできる。
から判定することもできる。
問題11−5
微分方程式
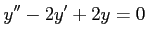 の特性方程式の解は
の特性方程式の解は
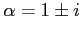 だから,
だから,
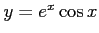 と
と
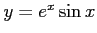 がこの微分方程式の基本解である.
がこの微分方程式の基本解である.
さらに,微分方程式
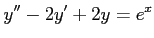 を解くには,
を解くには,
だから,
が解である.
解答 正


Next: 演習問題12解答
Up: 目次
Previous: 演習問題10解答