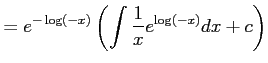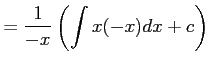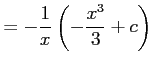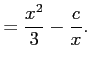

Next: 演習問題11解答
Up: 目次
Previous: 演習問題9解答
次のそれぞれの正誤を判定しなさい。
問題10−1
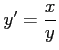 を解くには
を解くには
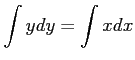 だから
だから
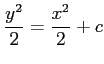 となり
となり
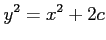 となり
となり
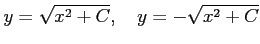 が解である.ただし,
が解である.ただし,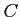 は定数.
は定数.
解答 正
問題10−2
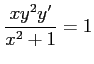 は変数分離形の微分方程式である.
は変数分離形の微分方程式である.
解答 正
コメント 実際、
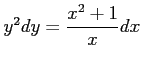 と変数分離できる。
と変数分離できる。
問題10−3
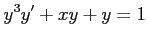 は変数分離形の微分方程式である.
は変数分離形の微分方程式である.
解答 誤
コメント
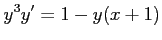 と書き直しても、右辺が
と書き直しても、右辺が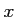 の関数と
の関数と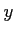 の関数の積に書き直せない。
の関数の積に書き直せない。
問題10−4
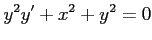 は同次形の微分方程式である.
は同次形の微分方程式である.
解答 正
コメント 実際、
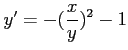 と書き直せる。
と書き直せる。
問題10−5
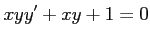 は同次形の微分方程式である.
は同次形の微分方程式である.
解答 誤
コメント 実際、
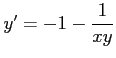 と書き直しても、右辺が
と書き直しても、右辺が
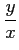 の関数とならない。
の関数とならない。
問題10−6
1階線形微分方程式
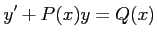 の解の公式は
の解の公式は
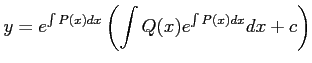 である.
である.
解答 誤
コメント 正しくは、
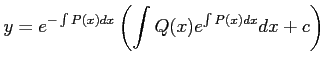
問題10−7
1階線形微分方程式
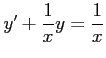 を
を 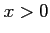 の範囲で解くと,
の範囲で解くと,
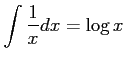 だから,解の公式より
だから,解の公式より
解答 正
問題10−8
1階線形微分方程式
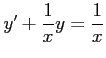 を
を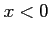 の範囲で解くと
の範囲で解くと
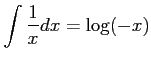 だから,解の公式より
だから,解の公式より
解答 正


Next: 演習問題11解答
Up: 目次
Previous: 演習問題9解答
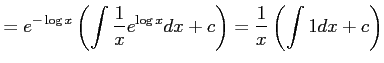
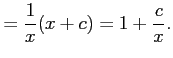
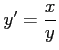 を解くには
を解くには
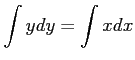 だから
だから
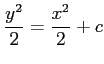 となり
となり
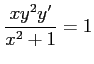 は変数分離形の微分方程式である.
は変数分離形の微分方程式である.
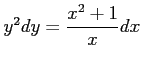 と変数分離できる。
と変数分離できる。
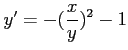 と書き直せる。
と書き直せる。
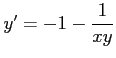 と書き直しても、右辺が
と書き直しても、右辺が
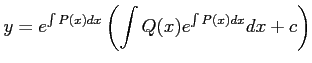 である.
である.
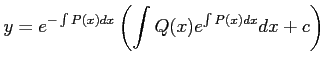
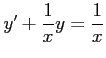 を
を 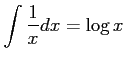 だから,解の公式より
だから,解の公式より
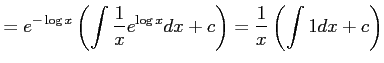
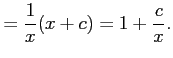
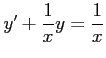 を
を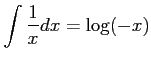 だから,解の公式より
だから,解の公式より