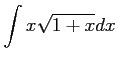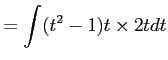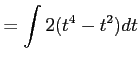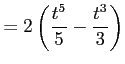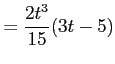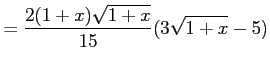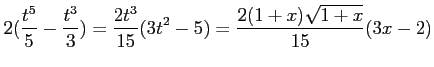

Next: 演習問題10解答
Up: 目次
Previous: 演習問題8解答
次のそれぞれの正誤を判定しなさい。
問題9−1
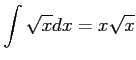
解答 誤
コメント
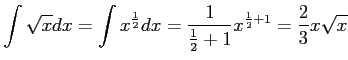
問題9−2
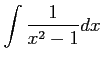 |
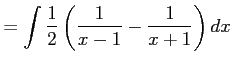 |
|
| |
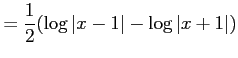 |
|
| |
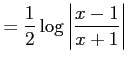 |
|
解答 正
問題9−3
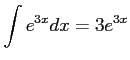
解答 誤
コメント
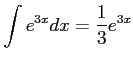
問題9−4
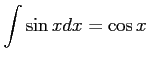
解答 誤
コメント
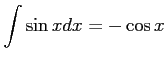
問題9−5
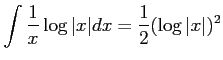
解答 正
コメント 部分積分の公式より、
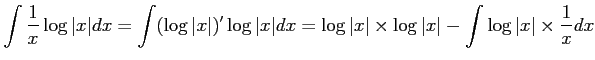
となり、移項することによって得られる。
問題9−6
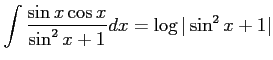
解答 誤
コメント
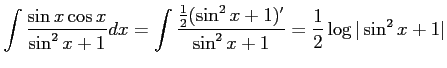
問題9−7
部分積分の公式は
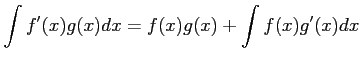 である.
である.
解答 誤
コメント 符号が間違っている。
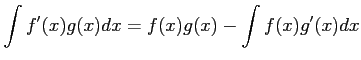
問題9−8
置換積分の公式は
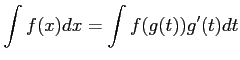 である.
である.
解答 正
問題9−9
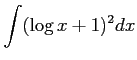 |
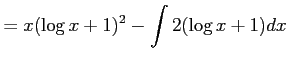 |
|
| |
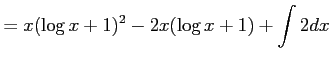 |
|
| |
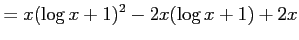 |
|
解答 正
問題9−10
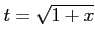 とおくと,
とおくと,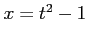 ,
,
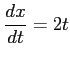 であるから
であるから
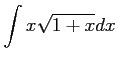 |
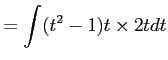 |
|
| |
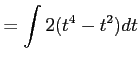 |
|
| |
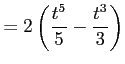 |
|
| |
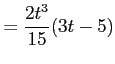 |
|
| |
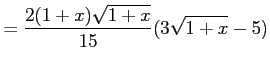 |
|
解答 誤
コメント


Next: 演習問題10解答
Up: sekibun
Previous: 演習問題8解答
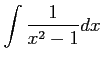
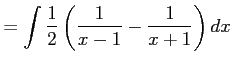
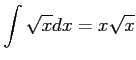
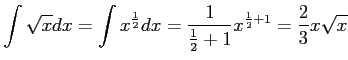
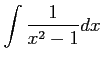
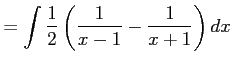
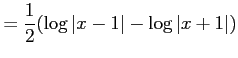
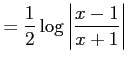
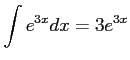
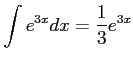
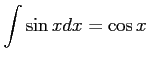
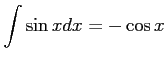
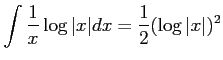
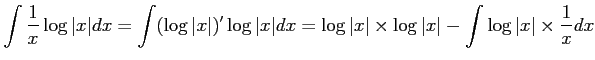
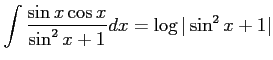
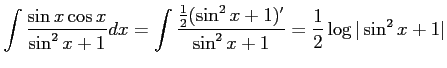
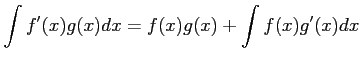 である.
である.
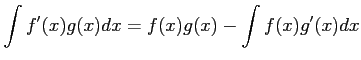
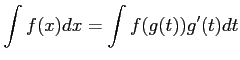 である.
である.
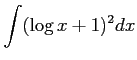
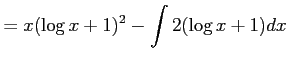
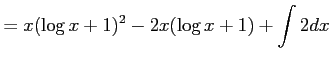
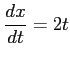 であるから
であるから