


Next: 演習問題4解答
Up: 目次
Previous: 演習問題2解答
次のそれぞれの正誤を判定しなさい。
問題3−1
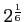 とは
とは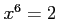 を満たす数
を満たす数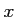 のことである.
のことである.
解答 誤
コメント 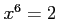 をみたす
をみたす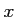 は正数と負数の2つあり、そのうち正数のほうが
は正数と負数の2つあり、そのうち正数のほうが
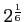 である。
である。
問題3−2
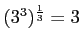
解答 正
コメント
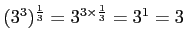
問題3−3
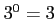
解答 誤
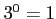 である。すべての正数
である。すべての正数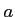 について
について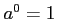 である。
である。
問題3−4
関数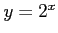 の値域は
の値域は
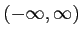 である.
である.
解答 誤
コメント 値域は
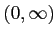 である。
である。
問題3−5
2つの実数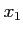 ,
,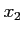 に対して
に対して
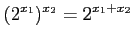 が成り立つ.
が成り立つ.
解答 誤
コメント
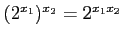
問題3−6
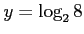 とすれば,
とすれば,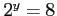 であるから
であるから
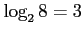 である.
である.
解答 正
コメント
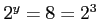 だから、
だから、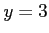
問題3−7
関数
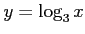 は関数
は関数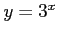 の逆関数である.
の逆関数である.
解答 正
問題3−8
2つの実数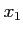 ,
,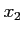 に対して
に対して
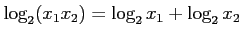
解答 誤
コメント 関数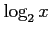 の定義域は
の定義域は
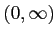 だから、
だから、
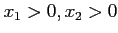 でなければならない。
でなければならない。
問題3−9
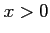 のとき
のとき
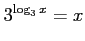
解答 正
コメント
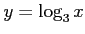 とおくと、
とおくと、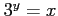 だから、
だから、
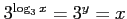
問題3−10
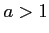 のとき関数
のとき関数
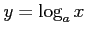 の値域は
の値域は
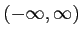 である.
である.
解答 正
問題3−11
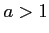 のとき
のとき
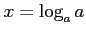 とおくと,
とおくと,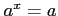 であるから
であるから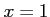 ,すなわち
,すなわち
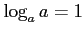 である.
である.
解答 正
問題3−12
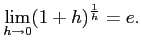
解答 正
コメント
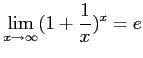 において、
において、
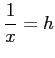 とおけば、
とおけば、
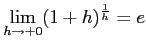 。
。
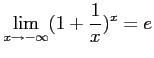 において、
において、
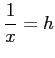 とおけば、
とおけば、
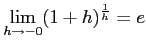 。
。
ゆえに、
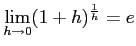 。
。



Next: 演習問題4解答
Up: 目次
Previous: 演習問題2解答
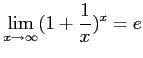 において、
において、
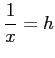 とおけば、
とおけば、
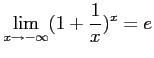 において、
において、
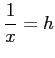 とおけば、
とおけば、