

Next: 演習問題5解答
Up: 目次
Previous: 演習問題3解答
次のそれぞれの正誤を判定しなさい。
問題4−1
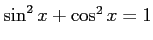
解答 正
問題4−2
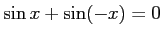
解答 正
コメント
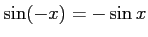 より。
より。
問題4−3
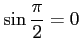
解答 誤
コメント
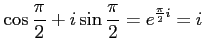 より、
より、
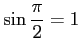
問題4−4
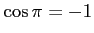
解答 正
コメント
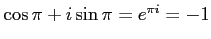 より、
より、
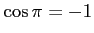
問題4−5
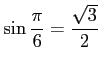
解答 誤
コメント
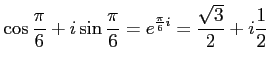 より、
より、
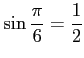
問題4−6
関数
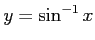 は関数
は関数
![$ y=\sin x (x \in[-\pi/2,\pi/2])$](img155.png) の逆関数である.
の逆関数である.
解答 正
問題4−7
関数
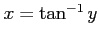 は関数
は関数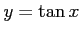 の逆関数である.
の逆関数である.
解答 誤
コメント
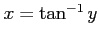 は
は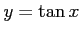
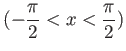 の逆関数である.
の逆関数である.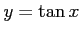 は逆関数を持たない。
は逆関数を持たない。
問題4−8
関数
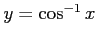 は単調減少関数で,値域は
は単調減少関数で,値域は![$ [0,\pi]$](img160.png) である.
である.
解答 正
問題4−9
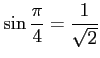 だから,
だから,
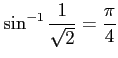 である.
である.
解答 正
問題4−10
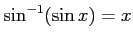
解答 誤
コメント
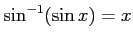
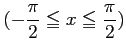 と制限すれば正しい。
と制限すれば正しい。
問題4−11
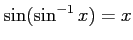
解答 正


Next: 演習問題5解答
Up: 目次
Previous: 演習問題3解答
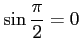
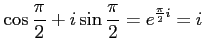 より、
より、
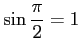
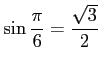
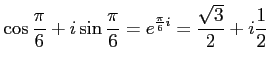 より、
より、
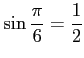
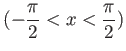 の逆関数である.
の逆関数である.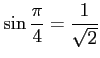 だから,
だから,
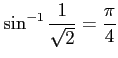 である.
である.
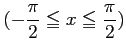 と制限すれば正しい。
と制限すれば正しい。