

Next: 演習問題6解答
Up: 目次
Previous: 演習問題4解答
次のそれぞれの正誤を判定しなさい。
問題5−1
定数関数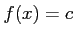 について,
について,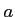 を定数とするとき
を定数とするとき
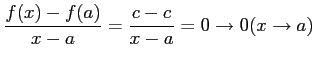 であるから
であるから
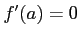 が成り立つ.したがって,
が成り立つ.したがって,
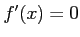 である.
である.
解答 正
問題5−2
関数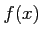 の導関数
の導関数
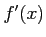 があるとき,
があるとき,
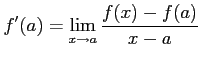 が成り立つ.
が成り立つ.
解答 正
問題5−3
どんな関数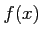 に対しても
に対しても
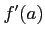 が定まる.
が定まる.
解答 誤
コメント 例えば、関数 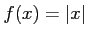 については、
については、
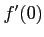 は存在しない。
は存在しない。
問題5−4
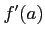 は関数
は関数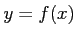 のグラフ上の点
のグラフ上の点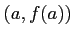 における接線の傾きである.
における接線の傾きである.
解答 正
問題5−5
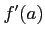 は関数
は関数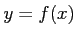 の
の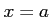 における「瞬間変化率」を意味する.
における「瞬間変化率」を意味する.
解答 正
問題5−6
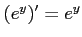
解答 正
コメント
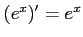 の変数を書き換えただけである。
の変数を書き換えただけである。
問題5−7
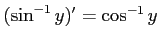
解答 誤
コメント
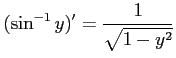
問題5−8
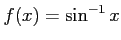 の
の
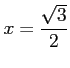 における微分係数は
における微分係数は
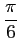 である.
である.
解答 誤
コメント
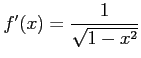 だから、
だから、
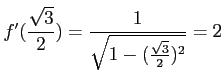
問題5−9
関数
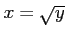 は関数
は関数
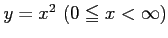 の逆関数であるから
の逆関数であるから
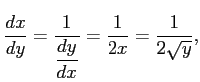 すなわち,
すなわち,
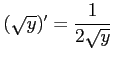 が成り立つ.
が成り立つ.
解答 正


Next: 演習問題6解答
Up: 目次
Previous: 演習問題4解答
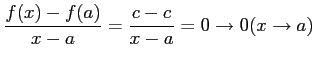 であるから
であるから
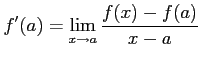 が成り立つ.
が成り立つ.
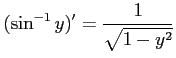
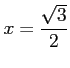 における微分係数は
における微分係数は
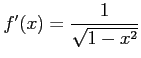 だから、
だから、
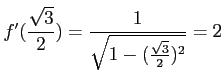
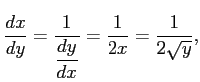 すなわち,
すなわち,
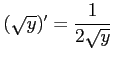 が成り立つ.
が成り立つ.