

Next: 演習問題7解答
Up: 目次
Previous: 演習問題5解答
次のそれぞれの正誤を判定しなさい。
問題6−1
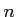 を自然数とするとき,関数
を自然数とするとき,関数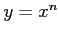 の値域は
の値域は
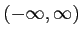 である.また導関数は
である.また導関数は
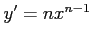 である.
である.
解答 誤
コメント 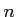 が偶数のときの値域は
が偶数のときの値域は
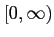 である。
である。
問題6−2
指数関数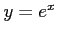 の定義域は
の定義域は
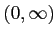 であり,値域は
であり,値域は
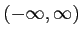 である.また導関数は
である.また導関数は
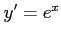 である.
である.
解答 誤
コメント 定義域は
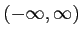 、値域は
、値域は
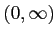 である。
である。
問題6−3
対数関数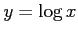 の定義域は
の定義域は
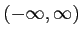 であり,値域は
であり,値域は
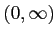 である.また導関数は
である.また導関数は
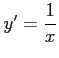 である.
である.
解答 誤
コメント 定義域が
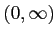 で、値域が
で、値域が
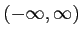 である。
である。
問題6−4
余弦関数 の値域は
の値域は![$ [0,1]$](img199.png) であり,導関数は
であり,導関数は
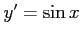 である.
である.
解答 誤
コメント 値域は![$ [-1,1]$](img201.png) であり、導関数は
であり、導関数は
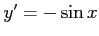 である。
である。
問題6−5
アークサイン関数
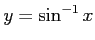 の定義域は
の定義域は![$ [-1,1]$](img201.png) であり,値域は
であり,値域は![$ [0,\pi]$](img160.png) である.また,導関数は
である.また,導関数は
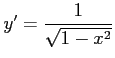 である.
である.
解答 誤
コメント 値域は
![$ [-\displaystyle \frac{\pi}{2},\frac{\pi}{2}]$](img204.png) である。
である。
問題6−6
アークタンジェント関数
 の値域は
の値域は
![$ [-\displaystyle \frac{\pi}{2},\frac{\pi}{2}]$](img204.png) であり,狭義単調増加である.
であり,狭義単調増加である.
解答 誤
コメント 値域は
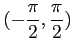 である。
である。
問題6−7
アークサイン関数とアークコサイン関数の間には
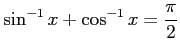 の関係がある.
の関係がある.
解答 正
問題6−8
関数
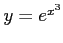 は関数
は関数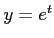 と関数
と関数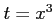 を合成してできる.
を合成してできる.
解答 正
問題6−9
関数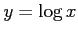 と関数
と関数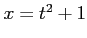 を合成すると関数
を合成すると関数
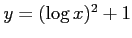 ができる.
ができる.
解答 誤
コメント 合成関数は
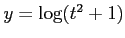 である。
である。
問題6−10
関数
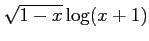 の定義域は
の定義域は![$ [-1,1]$](img201.png) である.
である.
解答 誤
コメント 関数
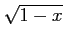 の定義域は
の定義域は
![$ (-\infty,1]$](img216.png) であり、関数
であり、関数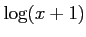 の定義域は
の定義域は
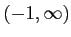 だから、
だから、
![$ (-\infty,1]\cap(-1,\infty)=(-1,1]$](img219.png) が定義域である。
が定義域である。
問題6−11
関数
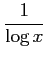 の定義域は
の定義域は
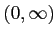 である.
である.
解答 誤
コメント 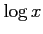 の定義域は
の定義域は
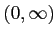 であるが、
であるが、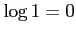 であるので、定義域は
であるので、定義域は
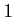 を取り除いた
を取り除いた
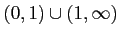 である。
である。


Next: 演習問題7解答
Up: 目次
Previous: 演習問題5解答
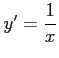 である.
である.
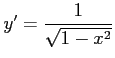 である.
である.
![$ [-\displaystyle \frac{\pi}{2},\frac{\pi}{2}]$](img204.png) である。
である。
![$ [-\displaystyle \frac{\pi}{2},\frac{\pi}{2}]$](img204.png) であり,狭義単調増加である.
であり,狭義単調増加である.
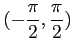 である。
である。
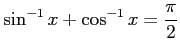 の関係がある.
の関係がある.