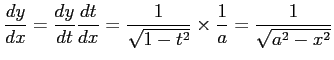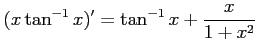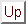

Next: 演習問題8解答
Up: 目次
Previous: 演習問題6解答
次のそれぞれの正誤を判定しなさい。
問題7−1
解答 誤
コメント
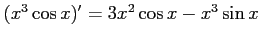
問題7−2
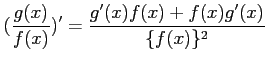
解答 誤
コメント
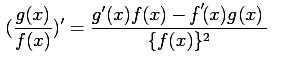
問題7−3
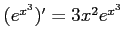
解答 正
問題7−4
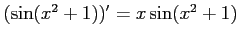
解答 誤
コメント 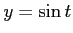 と
と 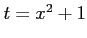 の合成関数だから、
の合成関数だから、
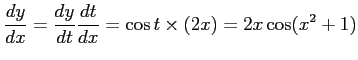
問題7−5
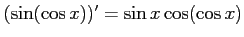
解答 誤
コメント 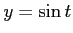 と
と 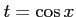 の合成関数だから、
の合成関数だから、
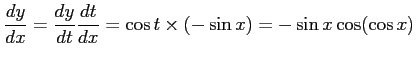
問題7−6
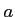 を正の定数とするとき
を正の定数とするとき
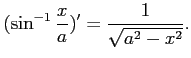
解答 正
コメント
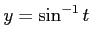 と
と
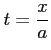 の合成関数だから、
の合成関数だから、
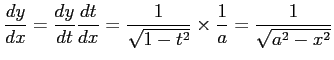
問題7−7
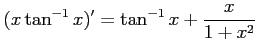
解答 正
コメント 関数の積の導関数の公式を用いる。
問題7−8
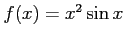 とすると
とすると
解答 誤
コメント
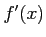 は正しい。
は正しい。
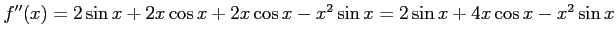
問題7−9
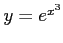 とするとき
とするとき
解答 正


Next: 演習問題8解答
Up: 目次
Previous: 演習問題6解答
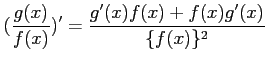
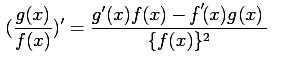
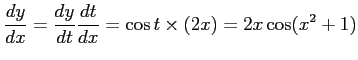
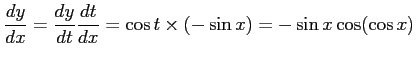
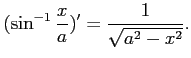
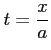 の合成関数だから、
の合成関数だから、