

Next: 演習問題9解答
Up: 目次
Previous: 演習問題7解答
次のそれぞれの正誤を判定しなさい。
問題8−1
関数
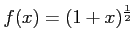 について
について
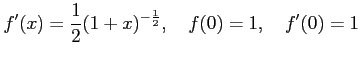 だから
だから
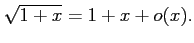
解答 誤
コメント
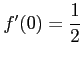 だから、
だから、
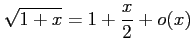
問題8−2
関数
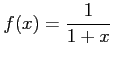 について
について
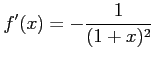 だから
だから
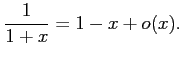
解答 正
問題8−3
関数
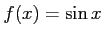 について,
について,
だから
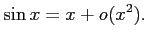
解答 正
問題8−4
関数
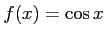 に対して
に対して
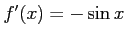 であるから
であるから
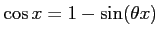 を満たす
を満たす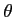 (
(
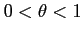 )が存在する.
)が存在する.
解答 誤
コメント
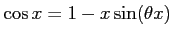 を満たす
を満たす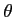 (
(
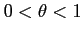 )が存在する.
)が存在する.
問題8−5
関数
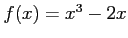 について
について
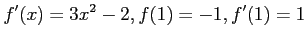 だから
だから
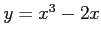 の点
の点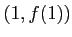 における接線の方程式は
における接線の方程式は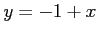 である.
である.
解答 誤
コメント 接線の方程式は
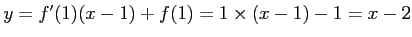 である。
である。
問題8−6
関数
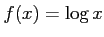 について
について
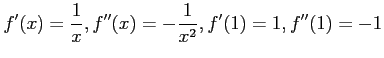 だから,
だから,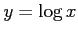 のグラフは点
のグラフは点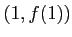 において,下に凸である.
において,下に凸である.
解答 誤
コメント
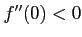 だから、上に凸である。
だから、上に凸である。
問題8−7
関数
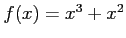 について
について
だからこの関数は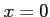 において極大値0をとる.
において極大値0をとる.
解答 誤
コメント
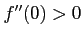 だから、
だから、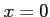 において極小値をとる。
において極小値をとる。
問題8−8
関数
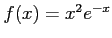 について
について
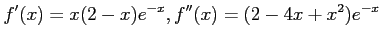 だから極大値または極小値をとる点の候補は
だから極大値または極小値をとる点の候補は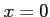 と
と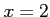 であり,
であり,
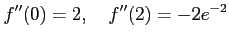 だから,この関数は
だから,この関数は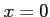 で極小値0,
で極小値0,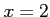 で極大値
で極大値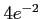 をとる.
をとる.
解答 正


Next: 演習問題9解答
Up: 目次
Previous: 演習問題7解答
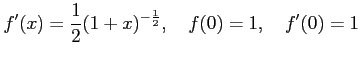 だから
だから
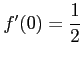 だから、
だから、
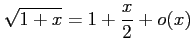
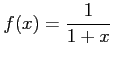 について
について
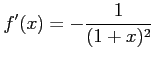 だから
だから
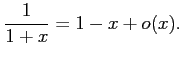
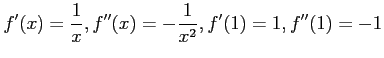 だから,
だから,